Umformung von Determinanten
Literaturangabe: Die folgenden Sätze über Determinanten entnehme ich dem Buch
v. Mangoldt – Knopp „Einführung in die Höhere Matheamtik“ – S. Hirzel Verlag Leipzig 1955
Satz 1: Wenn in einer Determinante alle Elemente einer Reihe gleich Null sind, so ist die Determinate selbst gleich Null.
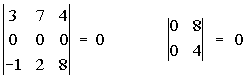
Satz 2: Wenn in einer Reihe alle Elemente gleich 0 sind bis auf eins, so ist die Determenante gleich dem Produkt diese einen Elements und einer Determinante, die um eine Ordnung niedriger ist. (Diese Determinante bildest du, indem du die Zeile und die Spalte wegläßt, in der dieses Element steht.)
Beispiel:
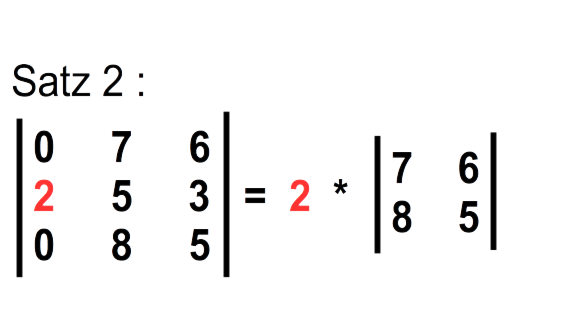
Satz 3 (Additionssatz): Wenn sich die Elemente einer Reihe als Summe von zwei Summanden darstellen lassen, dann ist die Determinante gleich der Summe von zwei Determinanten, in denen in der betreffenden Reihe jeweils einer der Summanden erscheint.
Beispiel:
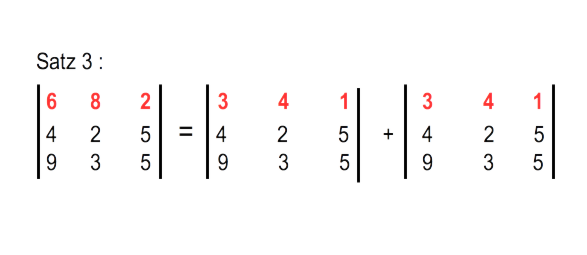
Die Elemente der ersten Zeile wurden in jeweils 2 Summanden zerlegt.
Satz 4 (Faktorsatz): Werden alle Elemente einer Reihe mit einer Zahl multipliziert, so wird dadurch auch der Wert der Determinante mit dieser Zahl multipliziert.
Beispiel für den Faktorsatz:

Satz 5 (Allgemeiner Nullsatz) : Wenn in einer Determinante die Elemente einer Reihe den gleichstelligen Elementen einer anderen, parallelen Reihe proportional sind, so hat die Determinante den Wert Null. In dem Beispiel sind die Zahlen der 4. Zeile jeweils das Dreifache der Zahlen in der 2. Zeile.
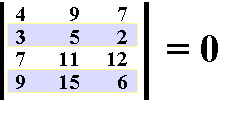
Satz 6 (Erhaltungssatz) : Eine Determinante bleibt ihrem Wert nach unverändert, wenn man zu allen Elementen einer Reihe ein und dasselbe Vielfache der gleichstelligen Elemente einer anderen, parallelen Reihe addiert.
Durch geschickte Anwendung dieses Satzes kann man einzelne Elemente der Determinante zu Nullen umwandeln. Dadurch wird die Berechnung des Wertes der Determinante erleichtert.
Beispiel:
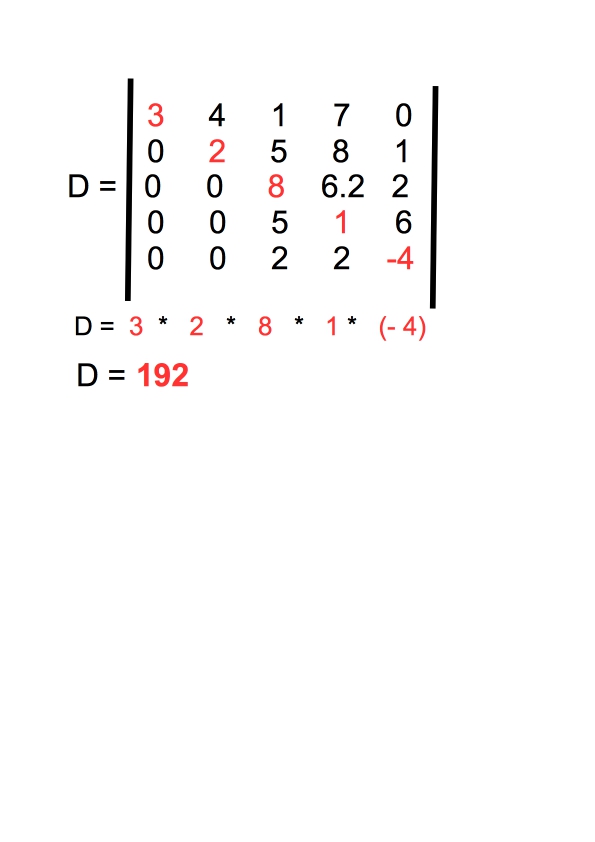
Ziel der Manipulationen ist eine „Dreiecksdeterminante“, bei welcher alle Zahlen unter der Hauptdiagonale gleich 0 sind.
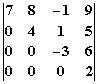
Der Wert der Dreiecksdeterminante ist gleich dem Produkt der Zahlen in der Hauptdiagonale. In diesem Fall also 7 * 4 * (-3) *2 = -168
Vertauschungssatz: Zwei Determinanten, von denen die eine aus der anderen durch Vertauschung von zwei parallelen Reihen entsteht, haben entgegengesetzt gleiche Werte. In dem Beispiel wurden die erste und die vierte Zeile vertauscht.
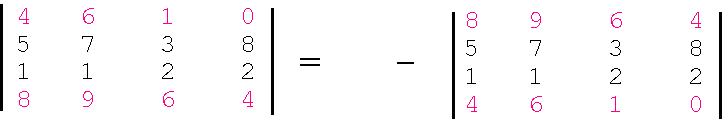
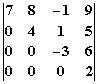
Dreiecksdeterminante
Weiter zu Lösung von Gleichungssystemen – Cramersche Regel http://klissh.de/?page_id=130