→
| 4. Determinanten höherer Ordnung – Unterdeterminanten (Adjunkten) |
| Eine Determinante der Ordnung 4

Unterdeterminanten (Adjunkten)
Entwicklung nach der ersten Spalte

Die Adjunkten einer Determinante entwickelt man, indem man die jeweilige Zeile und Spalte streicht und die übrig gebliebenen Zahlen in die Unterdeterminante überträgt.
Das Vorzeichen der Adjunkte wechselt nach dem folgenden Schema:
+ – + – +
– + – + –
+ – + – +
– + – + –
+ – + – +
Zeilennummer + Spaltennummer gerade → +
Zeilennummer + Spaltennummer ungerade → – |
So erhält man Determinanten, die immer eine Ordnung niedriger sind.
Aus einer Determinante der Ordnung 5 ergeben sich 5 Determinanten der Ordnung 4. Diese ergeben je 4 Determinanten der Ordnung 3. Und aus den Determinanten der Ordnung 3 ergeben sich je 3 kleine Determinanten der 2. Ordnung.Die Determinanten der 3. Ordnung lassen sich mit dem Satz von Sarrus berechnen.
Ein Beispiel für die Berechnung einer Determinante der Ordnung 4:

|
| Die Berechnung einer Determinante höherer Ordnung mit Hilfe der Unterdeterminanten ( Adjunkten) ist aufwendig. Wegen des Vorzeichenwechsels ist die Wahrscheinlichkeit hoch, daß man sich verrechnet. Für den Computer ist diese Methode aber gut geeignet. Der Computer ist eine Maschine. Er verrechnet sich nicht.
Wenn du eine Determinante „von Hand“. berechnen willst, empfiehlt sich eine andere Methode: Umwandlung in eine Dreiecksdeterminante.
Manipulation der Determinante bis in der linken oberen Ecke eine Zahl verschieden von Null steht. Die Stellen unter der Hauptdiagonalen sind 0. (Dreiecksdeterminante) Das Ergebnis ist das Produkt der Zahlen in der Hauptdiagonale. Die Zahlen über der Hauptdiagonale sind ohne Bedeutung.
D = 8 * 1 * 9 * 2
D = 144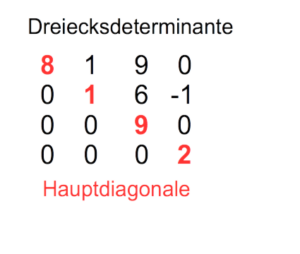
|
Weiter zu 1.5 – Umformung von Determinanten http://klissh.de/?page_id=127