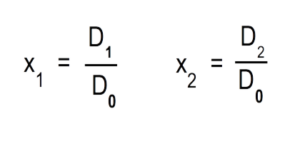Lösung von Gleichungssystemen – Cramersche Regel
|
|
||
| Lösung von Gleichungssystemen mit Determinanten – Cramersche Regel
Beispiel: Das folgende Gleichungssystem ist zu berechnen: 7 * x1 + 3 * x2 + 0 * x3 = 120 2 * x1 + 3 * x2 + 4 * x3 = 20 -2 * x1 + 0 * x2 + 5 * x3 = -70 Schreibe das Gleichungssystem als Matrix! (Die Unbekannten ordnen. In die letzte Spalte gehören die Zahlen ohne x.) Die Matrix 7 3 0 120 2 3 4 20 -2 0 5 -70 Bilde folgende Determinanten aus der Matrix:D0 = Die Spalten 1, 2, 3 7 3 0 2 3 4 -2 0 5 D1 = Die Spalten 4, 2, 3 120 3 0 20 3 4 -70 0 5 D2 = Die Spalten 1, 4, 3
7 3 120 2 3 20 -2 0 -70 Lösungsschema für die Berechnung von x1, x2 . . .
Bei Gleichungssystemen mit mehreren Unbekannten wird analog verfahren. Bei Gleichungssystemen mit mehrere Unbekannten kann die Rechenzeit lang werden! Im Fall D0 = 0 hat das Gleichungssystem keine Lösung.
|
||
Erläuterungen:
|