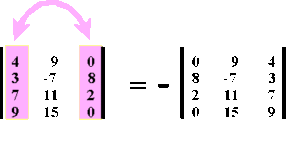- 7. Rechnen mit Determinanten
-
Eine Determinante hat den Wert 0, wenn in einer Zeile oder Spalte nur Nullen stehen.
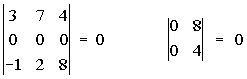
Wenn alle Elemente in zwei parallelen Zeilen oder Spalten gleich oder proportional sind, hat die Determinante den Wert 0.
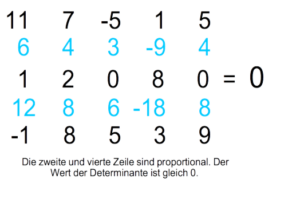Die zweite und die vierte Zeile sind proportional.
c.) Das „Stürzen“ einer Determinante. Wenn man die Elemente einer Determinante an der Hauptdiagonale spiegelt, ändert sich der Wert nicht.
-
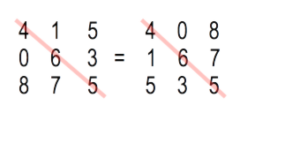
Wenn man zwei parallele Zeilen oder Spalten miteinander vertauscht, ändert sich das Vorzeichen:
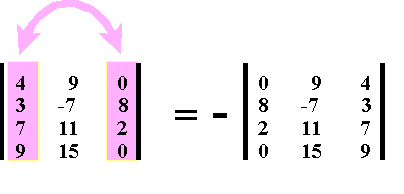
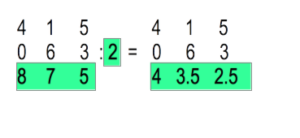
e.) Multiplikation von Determinanten: Eine Determinante wird mit einem Faktor multipliziert, indem man alle Elemente einer beliebigen Spalte oder Zeile mit diesem Faktor multipliziert.
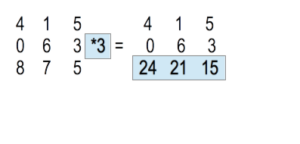
In diesem Fall wurden die Elemente der 3. Zeile mit 3 multipliziert.
-
- f.) Division: Eine Determinante wird dividiert, indem alle Elemente einer Zeile oder einer Spalte durch dieselbe Zahl dividiert werden.
-
- Wenn alle Elemente einer Zeile oder Spalte einen Faktor enthalten, kann dieser vor die Determinante gezogen werden. ( „Ausklammern“ )
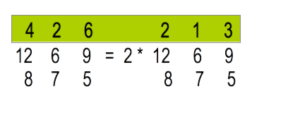In diesem Fall enthalten alle Elemente der 1 Zeile den Fakter 2. Dieser kann vor die Determinante gezogen werden. -
- Addition bzw. Subtraktion von Zeilen oder Spalten – Berechnung einer Determinante
- Man kann eine Zeile oder Spalte zu einer parallelen Zeile oder Spalte addieren ohne den Wert der Determinante zu ändern. Ich addiere die erste Zeile zur vierten Zeile. Unten links erscheint eine 0.
- Durch Manipulation der Zeilen und Spalten kann man den Wert einer Determinante berechnen. Ziel ist eine „Dreiecksdeterminante“. In diesem Fall habe ich die erste Zeile zur vierten Zeile addiert. Als Folge ist nun unten links eine 0 aufgetaucht. Für die Berechnung von Determinanten „von Hand“ ist es günstig, durch entsprechende Manipulation möglichst viele Nullen zu erhalten.
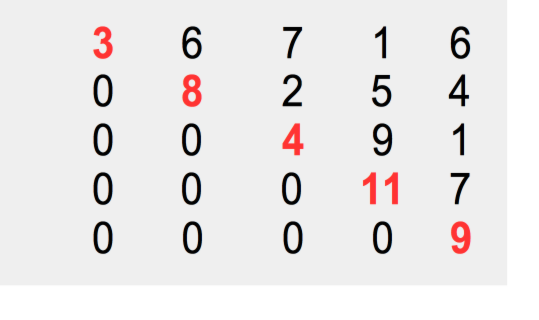
Dreiecksdeterminante - Unter der Hauptdiagonale (rot) stehen nur Nullen. Der Wert der Determinante ist das Produkt der Zahlen in der Hauptdiagonale
- 3 * 8 * 4 * 9 = 864
-
- Man kann auch eine Zeile oder Spalte zunächst mit einer Zahl multiplizieren und dann zu einer anderen Zeile oder Spalte addieren.
- In diesem Beispiel habe ich die erste Zeile mit (-1) multipliziert und dann zur dritten Zeile addiert.
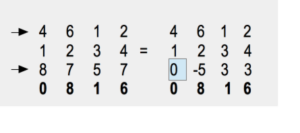
- Die „8“ in der zweiten Spalte kann man durch eine Null ersetzen, indem man die ganze dritte Spalte mit (-8) multipliziert und dann zur zweiten Spalte addiert.
- Und so sieht die Determinante nun aus:
- 4 6 1 2
- 1 2 3 4
- 0 -5 3 3
- 0 0 1 6
Die „6“ in der untersten Reihe kann ich durch eine „0“ ersetzen, indem ich die dritte Spalte mit (-6) multipliziere und zur vierten Spalte addiere. Das ergibt diese Determinante:
4 6 1 -4 1. 2 3 -14 0 -5 3 -15 0 0 1 0 In der vierten Zeile stehen nun Nullen und eine 1. Daraus lässt sich die Unterdeterminante bilden, indem man die 3. Spalte und die 4. Zeile weglässt:
4 6 -4
1 * 1 2 -14
0 -5 -15
