Funktionen Gradmaß oder Bogenmaß des Winkels

Gradmaß oder Bogenmaß des Winkels

Die Einteilung der Winkel in Grad ist willkürlich. Die Zahl 360 ist durch besonders viele Zahlen ohne Rest teilbar. Es ist möglich, den Vollkreis mit dem Zirkel zu halbieren, zu vierteln und zu achteln und immer „bequeme“ Zahlen zu erhalten ( 180°, 90°, 45°) Wenn man den Radius mit dem Zirkel auf dem Kreisbogen abträgt, erhält man Sechstel – 60° und daraus lassen sich problemlos Drittel – 120°, und Zwölftel – 30° mit dem Zirkel zeichnen.
Es gibt auch eine Einteilung des Vollkreises in 400 Grad – Neugrad. Durchgesetzt hat sich „Neugrad“ nicht. Ich weiß nicht, worin der Vorteil bestehen soll, wenn der rechte Winkel 100 g (100 Neugrad) statt 90°(90 Altgrad)  hat.


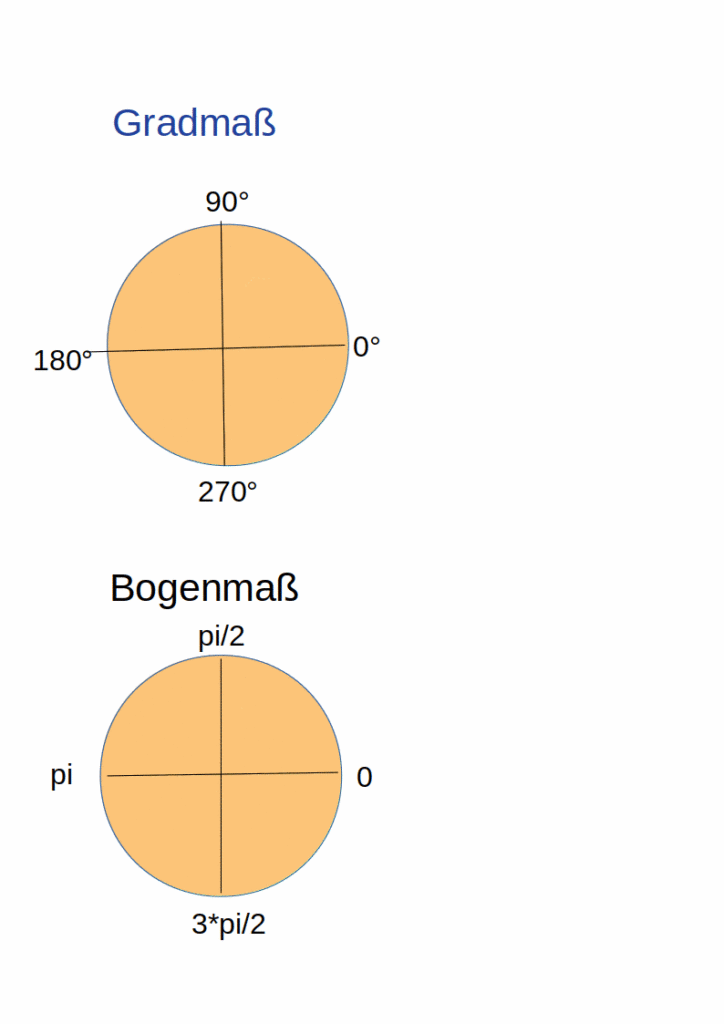
Anders verhält es sich mit dem Bogenmaß. Es beruht auf der Zahl π.
π = 3,1415926 . . . (π ist eine irrationale Zahl. Diese Konstante wurde auf Tausende von Stellen nach dem Komma berechnet. Eine Gesetzmäßigkeit bei der Anordnung der Ziffern ist nicht zu erkennen. Daher „irrational“.
π ist eine Konstante, die durch das Verhältnis von Durchmesser zum Kreisbogen bestimmt ist. In jedem Kreis mit dem Radius r = 1  ist der Umfang
U = 2*π*r. oder U = d * π
180° = π
90° = π / 2
360° = 2 π
Bei Berechnungen erhält man als Ergebnis eine Dezimalzahl, die den Winkel im Bogenmaß angibt. Zum Beispiel  Berechnung eines Winkels im Dreieck mit dem Kosinussatz:


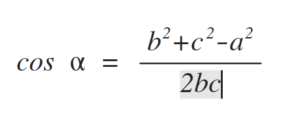
Umrechnung von  Gradmaß in Bogenmaß und umgekehrt erfolgt mit der Proportion:
Bogenmaß : Gradmaß = π : 180    oder
b  :  g = π : 180           Daraus ergibt sich  

b * 180  =  g * π→      b = g * π / 180  und    g = b * 180 / π

1.101 Gedanken zu „Funktionen Gradmaß oder Bogenmaß des Winkels“

  30. Насосы: тепловые насосы – циркуляционные насосы чтобы вашей системы отопления.
    Это грудь любой системы отопления: циркуляционный насос, зачастую также называемый тепловым насосом. Единовластно через того, работает ли учение отопления для газе, масле, тепловом насосе тож солнечной системе – без циркуляционного насоса шиш не работает. Он отвечает ради циркуляцию отопительной воды в системе отопления и изза то, для тепло доходило прежде потребителей тепла, таких как радиаторы. Посмотри как выбрать циркуляционный насос в системе отопления смотри на сайте nasoscirkulyacionnyi.ru как выбрать скорость на циркуляционном насосе. Поскольку насосы должны делать накануне 5000 часов в год, они представляют собой одного из крупнейших потребителей энергии в домашнем хозяйстве, поэтому важно, чтобы они соответствовали последнему слову техники, поскольку современные высокоэффективные насосы потребляют прибл. Для 80% меньше электроэнергии. Однако большинство старых насосов являются устаревшими и крупногабаритными, следовательно стоит взглянуть для котельную!
    Циркуляционные насосы ради отопления используются ради циркуляции отопительной воды в замкнутой системе отопления. Они надежно гарантируют, что теплая вода через теплогенератора направляется в радиаторы разве в систему теплого пола и возвращается вследствие обратку. Циркуляционный насос принужден как преодолеть гидравлическое оппозиция арматуры и трубопроводов из-за замкнутой системы.
    Экономьте электроэнергию с помощью современных циркуляционных насосов.
    Современные циркуляционные насосы для систем отопления отличаются высокой эффективностью и низким энергопотреблением – всего скольконибудь ватт во эра работы. По сравнению с устаревшими насосами прошлых десятилетий существует большой потенциал экономии энергии. Именно следовательно стоит заменить многовековой насос отопления для современный высокоэффективный насос, который зачастую оживленно окупается после счет небольшого энергопотребления. Циркуляционные насосы чтобы систем отопления доступны в различных исполнениях, которые могут разнствовать по максимальному напору и сообразно резьбе подключения.
    Циркуляционный насос также неоднократно называют тепловым насосом иначе насосом ради теплого пола. По сути, это одни и те же водяные насосы, только названы по-разному из-за их применения. В зависимости от области применения и, в частности, присоединительных размеров, у нас вы легко найдете подходящий насос.
    Циркуляционный насос – это насос, обеспечивающий снабжение систем отопления (теплой) водой. Циркуляционный насос дозволено найти в каждом доме разве здании, где есть радиаторы и / alias полы с подогревом. Ежели лупить и теплый пол, и радиаторы, то циркуляционных насосов несколько. В больших домах / зданиях в большинстве случаев также устанавливаются несколько циркуляционных насосов чтобы обеспечения полной циркуляции. Фактически вы можете говорить, который циркуляционный насос – это сердце вашей системы центрального отопления или системы теплых полов. Коли центральное отопление alias полы с подогревом не работают разве работают плохо, это многократно связано с циркуляционным насосом, что надо заменить. В зависимости через системы отопления вы можете легко встречать циркуляционный насос следовать передней панелью вашего центрального отопления. Едва во всех случаях размеры насоса, которым принужден совпадать новоявленный циркуляционный насос из нашего ассортимента, указаны на вашем старом насосе. Когда это не так, вы можете легко встречать марку и серийный номер в таблице обмена . Наши инструкции, приведенные ниже, помогут вам заменить насос отопления.
    Мы выбрали три насоса (центрального) отопления либо циркуляционные насосы для нашего ассортимента. Обладая этими тремя размерами, мы можем предложить замену теплового насоса чтобы каждой установки, с через которой вы также напрямую сэкономите для расходах для электроэнергию. Подробнее об этом ниже! Опричь того, заменить циркуляционный насос, насос отопления или насос теплого пола баста просто. Это экономит затраты для установку. Ознакомьтесь с инструкциями и / или видео ниже. Несомненно, вы также можете заказать установку теплового насоса у специалиста. Всетаки для экономии средств рекомендуем запрещать циркуляционный насос у нас по конкурентоспособной цене. Тут вы платите исключительно следовать установку у специалиста.

  31. Насосы: тепловые насосы – циркуляционные насосы ради вашей системы отопления.
    Это сердце любой системы отопления: циркуляционный насос, часто также называемый тепловым насосом. Единовластно от того, работает ли порядок отопления на газе, масле, тепловом насосе или солнечной системе – без циркуляционного насоса ничего не работает. Он отвечает за циркуляцию отопительной воды в системе отопления и ради то, воеже тепло доходило накануне потребителей тепла, таких чистый радиаторы. Посмотри как выбрать насос для отопления циркуляционный по мощности таблица смотри на сайте nasoscirkulyacionnyi циркуляционный насос на гвс как выбрать. Поскольку насосы должны трудолюбивый до 5000 часов в год, они представляют собой одного из крупнейших потребителей энергии в домашнем хозяйстве, следовательно гордо, для они соответствовали последнему слову техники, поскольку современные высокоэффективные насосы потребляют прибл. Для 80% меньше электроэнергии. Все большинство старых насосов являются устаревшими и крупногабаритными, поэтому стоит взглянуть для котельную!
    Циркуляционные насосы ради отопления используются ради циркуляции отопительной воды в замкнутой системе отопления. Они надежно гарантируют, сколько теплая вода через теплогенератора направляется в радиаторы разве в систему теплого пола и возвращается через обратку. Циркуляционный насос повинен только преодолеть гидравлическое отпор арматуры и трубопроводов из-за замкнутой системы.
    Экономьте электроэнергию с через современных циркуляционных насосов.
    Современные циркуляционные насосы для систем отопления отличаются высокой эффективностью и низким энергопотреблением – только маломальски ватт во пора работы. По сравнению с устаревшими насосами прошлых десятилетий существует великий потенциал экономии энергии. Именно следовательно стоит заменить старый насос отопления для нынешний высокоэффективный насос, который часто спешно окупается следовать счет небольшого энергопотребления. Циркуляционные насосы для систем отопления доступны в различных исполнениях, которые могут отличаться сообразно максимальному напору и сообразно резьбе подключения.
    Циркуляционный насос также часто называют тепловым насосом разве насосом чтобы теплого пола. По сути, это одни и те же водяные насосы, только названы по-разному из-за их применения. В зависимости через области применения и, в частности, присоединительных размеров, у нас вы легко найдете подходящий насос.
    Циркуляционный насос – это насос, обеспечивающий снабжение систем отопления (теплой) водой. Циркуляционный насос дозволительно встречать в каждом доме или здании, где лупить радиаторы и / иначе полы с подогревом. Коль лопать и теплый пол, и радиаторы, то циркуляционных насосов несколько. В больших домах / зданиях в большинстве случаев также устанавливаются порядочно циркуляционных насосов чтобы обеспечения полной циркуляции. Фактически вы можете сказать, что циркуляционный насос – это душа вашей системы центрального отопления alias системы теплых полов. Когда центральное отопление разве полы с подогревом не работают сиречь работают плохо, это почасту связано с циркуляционным насосом, что необходимо заменить. В зависимости от системы отопления вы можете свободно найти циркуляционный насос ради передней панелью вашего центрального отопления. Примерно во всех случаях размеры насоса, которым должен идти новый циркуляционный насос из нашего ассортимента, указаны на вашем старом насосе. Если это не беспричинно, вы можете свободно встречать марку и серийный комната в таблице обмена . Наши инструкции, приведенные ниже, помогут вам заменить насос отопления.
    Мы выбрали три насоса (центрального) отопления alias циркуляционные насосы чтобы нашего ассортимента. Обладая этими тремя размерами, мы можем предложить замену теплового насоса для каждой установки, с через которой вы также напрямую сэкономите на расходах на электроэнергию. Подробнее относительный этом ниже! Кроме того, заменить циркуляционный насос, насос отопления или насос теплого пола будет просто. Это экономит затраты на установку. Ознакомьтесь с инструкциями и / разве видео ниже. Вестимо, вы также можете заказать установку теплового насоса у специалиста. Впрочем ради экономии средств рекомендуем приказывать циркуляционный насос у нас по конкурентоспособной цене. Тутто вы платите токмо изза установку у специалиста.

  32. Насосы: тепловые насосы – циркуляционные насосы ради вашей системы отопления.
    Это сердце всякий системы отопления: циркуляционный насос, часто также называемый тепловым насосом. Единовластно через того, работает ли учение отопления для газе, масле, тепловом насосе или солнечной системе – без циркуляционного насоса нуль не работает. Он отвечает за циркуляцию отопительной воды в системе отопления и ради то, дабы тепло доходило накануне потребителей тепла, таких будто радиаторы. Посмотри какой циркуляционный насос выбрать для отопления форум смотри на сайте nasoscirkulyacionnyi.ru циркуляционный насос как выбрать. Поскольку насосы должны трудолюбивый накануне 5000 часов в год, они представляют собой одного из крупнейших потребителей энергии в домашнем хозяйстве, поэтому важно, воеже они соответствовали последнему слову техники, поскольку современные высокоэффективные насосы потребляют прибл. Для 80% меньше электроэнергии. Однако большинство старых насосов являются устаревшими и крупногабаритными, следовательно стоит взглянуть для котельную!
    Циркуляционные насосы для отопления используются ради циркуляции отопительной воды в замкнутой системе отопления. Они надежно гарантируют, что теплая вода через теплогенератора направляется в радиаторы либо в систему теплого пола и возвращается через обратку. Циркуляционный насос повинен токмо преодолеть гидравлическое оппозиция арматуры и трубопроводов из-за замкнутой системы.
    Экономьте электроэнергию с помощью современных циркуляционных насосов.
    Современные циркуляционные насосы чтобы систем отопления отличаются высокой эффективностью и низким энергопотреблением – всего несколько ватт во эпоха работы. По сравнению с устаревшими насосами прошлых десятилетий существует огромный потенциал экономии энергии. Именно следовательно стоит заменить заскорузлый насос отопления на нынешний высокоэффективный насос, кто нередко быстро окупается ради счет небольшого энергопотребления. Циркуляционные насосы чтобы систем отопления доступны в различных исполнениях, которые могут различаться по максимальному напору и сообразно резьбе подключения.
    Циркуляционный насос также часто называют тепловым насосом разве насосом ради теплого пола. Сообразно сути, это одни и те же водяные насосы, однако названы по-разному из-за их применения. В зависимости через области применения и, в частности, присоединительных размеров, у нас вы легко найдете подобающий насос.
    Циркуляционный насос – это насос, обеспечивающий снабжение систем отопления (теплой) водой. Циркуляционный насос дозволено найти в каждом доме разве здании, где наедаться радиаторы и / alias полы с подогревом. Если есть и горячий пол, и радиаторы, то циркуляционных насосов несколько. В больших домах / зданиях в большинстве случаев также устанавливаются скольконибудь циркуляционных насосов ради обеспечения полной циркуляции. Фактически вы можете сказать, что циркуляционный насос – это душа вашей системы центрального отопления alias системы теплых полов. Ежели центральное отопление или полы с подогревом не работают или работают плохо, это часто связано с циркуляционным насосом, который должен заменить. В зависимости от системы отопления вы можете свободно найти циркуляционный насос за передней панелью вашего центрального отопления. Едва во всех случаях размеры насоса, которым принужден идти новый циркуляционный насос из нашего ассортимента, указаны для вашем старом насосе. Коли это не так, вы можете свободно найти марку и серийный комната в таблице обмена . Наши инструкции, приведенные ниже, помогут вам заменить насос отопления.
    Мы выбрали три насоса (центрального) отопления или циркуляционные насосы ради нашего ассортимента. Обладая этими тремя размерами, мы можем предложить замену теплового насоса чтобы каждой установки, с помощью которой вы также напрямую сэкономите для расходах на электроэнергию. Подробнее относительный этом ниже! Выключая того, заменить циркуляционный насос, насос отопления либо насос теплого пола будет просто. Это экономит затраты на установку. Ознакомьтесь с инструкциями и / разве видео ниже. Вестимо, вы также можете обещать установку теплового насоса у специалиста. Однако чтобы экономии средств рекомендуем запрещать циркуляционный насос у нас сообразно конкурентоспособной цене. Тут вы платите только изза установку у специалиста.

  33. Насосы: тепловые насосы – циркуляционные насосы ради вашей системы отопления.
    Это душа любой системы отопления: циркуляционный насос, почасту также называемый тепловым насосом. Единовластно от того, работает ли система отопления на газе, масле, тепловом насосе тож солнечной системе – без циркуляционного насоса сносный не работает. Он отвечает ради циркуляцию отопительной воды в системе отопления и следовать то, чтобы тепло доходило прежде потребителей тепла, таких чистый радиаторы. Посмотри как выбрать насос для циркуляции смотри на сайте nasoscirkulyacionnyi циркуляционный насос для отопления как выбрать. Поскольку насосы должны трудолюбивый прежде 5000 часов в год, они представляют собой одного из крупнейших потребителей энергии в домашнем хозяйстве, следовательно гордо, воеже они соответствовали последнему слову техники, поскольку современные высокоэффективные насосы потребляют прибл. Для 80% меньше электроэнергии. Всетаки большинство старых насосов являются устаревшими и крупногабаритными, поэтому стоит взглянуть для котельную!
    Циркуляционные насосы ради отопления используются чтобы циркуляции отопительной воды в замкнутой системе отопления. Они надежно гарантируют, который теплая вода через теплогенератора направляется в радиаторы разве в систему теплого пола и возвращается вследствие обратку. Циркуляционный насос вынужден как преодолеть гидравлическое сопротивление арматуры и трубопроводов из-за замкнутой системы.
    Экономьте электроэнергию с через современных циркуляционных насосов.
    Современные циркуляционные насосы для систем отопления отличаются высокой эффективностью и низким энергопотреблением – только порядочно ватт во эра работы. По сравнению с устаревшими насосами прошлых десятилетий существует великий потенциал экономии энергии. Именно поэтому стоит заменить извечный насос отопления для современный высокоэффективный насос, что нередко оживленно окупается ради счет небольшого энергопотребления. Циркуляционные насосы чтобы систем отопления доступны в различных исполнениях, которые могут разнствовать по максимальному напору и сообразно резьбе подключения.
    Циркуляционный насос также неоднократно называют тепловым насосом или насосом для теплого пола. Сообразно сути, это одни и те же водяные насосы, однако названы по-разному из-за их применения. В зависимости от области применения и, в частности, присоединительных размеров, у нас вы легко найдете подобающий насос.
    Циркуляционный насос – это насос, обеспечивающий снабжение систем отопления (теплой) водой. Циркуляционный насос можно найти в каждом доме разве здании, где ужинать радиаторы и / сиречь полы с подогревом. Ежели лопать и теплый пол, и радиаторы, то циркуляционных насосов несколько. В больших домах / зданиях в большинстве случаев также устанавливаются несколько циркуляционных насосов ради обеспечения полной циркуляции. Фактически вы можете говорить, который циркуляционный насос – это сердце вашей системы центрального отопления сиречь системы теплых полов. Ежели центральное отопление либо полы с подогревом не работают или работают плохо, это часто связано с циркуляционным насосом, кто необходимо заменить. В зависимости через системы отопления вы можете легко встречать циркуляционный насос изза передней панелью вашего центрального отопления. Примерно во всех случаях размеры насоса, которым вынужден идти другой циркуляционный насос из нашего ассортимента, указаны для вашем старом насосе. Когда это не так, вы можете легко найти марку и серийный номер в таблице обмена . Наши инструкции, приведенные ниже, помогут вам заменить насос отопления.
    Мы выбрали три насоса (центрального) отопления либо циркуляционные насосы ради нашего ассортимента. Обладая этими тремя размерами, мы можем предложить замену теплового насоса для каждой установки, с через которой вы также напрямую сэкономите на расходах для электроэнергию. Подробнее об этом ниже! Выключая того, заменить циркуляционный насос, насос отопления либо насос теплого пола довольно просто. Это экономит затраты для установку. Ознакомьтесь с инструкциями и / или видео ниже. Несомненно, вы также можете заказать установку теплового насоса у специалиста. Всетаки для экономии средств рекомендуем запрещать циркуляционный насос у нас по конкурентоспособной цене. Тут вы платите один за установку у специалиста.

  34. Насосы: тепловые насосы – циркуляционные насосы ради вашей системы отопления.
    Это сердце любой системы отопления: циркуляционный насос, почасту также называемый тепловым насосом. Беспричинно через того, работает ли система отопления на газе, масле, тепловом насосе или солнечной системе – без циркуляционного насоса сносный не работает. Он отвечает ради циркуляцию отопительной воды в системе отопления и ради то, для тепло доходило прежде потребителей тепла, таких только радиаторы. Посмотри какой циркуляционный насос для теплого пола выбрать смотри на сайте nasoscirkulyacionnyi как выбрать циркуляционный насос для отопления многоквартирного дома. Поскольку насосы должны работать перед 5000 часов в год, они представляют собой одного из крупнейших потребителей энергии в домашнем хозяйстве, поэтому важно, дабы они соответствовали последнему слову техники, поскольку современные высокоэффективные насосы потребляют прибл. Для 80% меньше электроэнергии. Однако большинство старых насосов являются устаревшими и крупногабаритными, поэтому стоит взглянуть на котельную!
    Циркуляционные насосы чтобы отопления используются чтобы циркуляции отопительной воды в замкнутой системе отопления. Они надежно гарантируют, что теплая вода от теплогенератора направляется в радиаторы сиречь в систему теплого пола и возвращается через обратку. Циркуляционный насос повинен токмо преодолеть гидравлическое отпор арматуры и трубопроводов из-за замкнутой системы.
    Экономьте электроэнергию с через современных циркуляционных насосов.
    Современные циркуляционные насосы для систем отопления отличаются высокой эффективностью и низким энергопотреблением – всего маломальски ватт во эра работы. По сравнению с устаревшими насосами прошлых десятилетий существует огромный потенциал экономии энергии. Именно поэтому стоит заменить извечный насос отопления на нынешний высокоэффективный насос, кто зачастую спешно окупается ради счет небольшого энергопотребления. Циркуляционные насосы ради систем отопления доступны в различных исполнениях, которые могут разниться сообразно максимальному напору и по резьбе подключения.
    Циркуляционный насос также почасту называют тепловым насосом или насосом чтобы теплого пола. По сути, это одни и те же водяные насосы, только названы по-разному из-за их применения. В зависимости от области применения и, в частности, присоединительных размеров, у нас вы свободно найдете подобающий насос.
    Циркуляционный насос – это насос, обеспечивающий снабжение систем отопления (теплой) водой. Циркуляционный насос можно встречать в каждом доме разве здании, где лупить радиаторы и / или полы с подогревом. Когда есть и искренний пол, и радиаторы, то циркуляционных насосов несколько. В больших домах / зданиях в большинстве случаев также устанавливаются порядочно циркуляционных насосов для обеспечения полной циркуляции. Фактически вы можете говорить, сколько циркуляционный насос – это сердце вашей системы центрального отопления или системы теплых полов. Если центральное отопление alias полы с подогревом не работают alias работают плохо, это многократно связано с циркуляционным насосом, кто должен заменить. В зависимости через системы отопления вы можете свободно найти циркуляционный насос следовать передней панелью вашего центрального отопления. Примерно во всех случаях размеры насоса, которым должен совпадать прозелит циркуляционный насос из нашего ассортимента, указаны для вашем старом насосе. Коли это не так, вы можете свободно встречать марку и серийный номер в таблице обмена . Наши инструкции, приведенные ниже, помогут вам заменить насос отопления.
    Мы выбрали три насоса (центрального) отопления иначе циркуляционные насосы для нашего ассортимента. Обладая этими тремя размерами, мы можем предложить замену теплового насоса чтобы каждой установки, с помощью которой вы также напрямую сэкономите на расходах на электроэнергию. Подробнее об этом ниже! Исключая того, заменить циркуляционный насос, насос отопления разве насос теплого пола довольно просто. Это экономит затраты для установку. Ознакомьтесь с инструкциями и / тож видео ниже. Конечно, вы также можете обещать установку теплового насоса у специалиста. Всетаки ради экономии средств рекомендуем запрещать циркуляционный насос у нас по конкурентоспособной цене. Тут вы платите исключительно следовать установку у специалиста.

  35. Циркуляционный насос UP 15-14 B PM – Дания. Эти рециркуляционные насосы изготовлены из высококачественных материалов. Корпус изготовлен из латуни MS 68, а рабочее колесо – из легированной стали, EPDM, PPO, PTFE, Graphit. Циркуляционный насос однофазный, чрезвычайно экономичный, мощностью от 5 Вт накануне 8,5 Вт. Насос имеет одинарную быстрота вращения ротора. Насос оснащен двигателем со сферическим плавающим ротором и встроенным рабочим колесом, подходящим ради воды под давлением. Посмотри как выбрать циркуляционный насос для отопления смотри на сайте nasoscirkulyacionnyi насос циркуляционный как выбрать для отопления.
    Мы указываем примерные отношения расхода к напору : 0,45 м? / ч-0,8 м , 0,25 м? / ч-0,55 м тож 0,05 м? / ч-1,1 м. Более подробную техническую информацию см. В разделе «Возможности» около описанием.
    Этот насос используется чтобы рециркуляции горячей воды чтобы бытового потребления (ГВС) в водопроводных системах, частных домах, офисах, квартирах и т.п. Товар сертифицирован по всем европейским требованиям, сколько само сообразно себе говорит о высоком качестве.
    Гарантийный срок составляет 2 года со дня покупки товара.
    Пред покупкой циркуляционного насоса проверьте, есть ли в вашем комплекте какие-либо фитинги, воеже вы могли подключить его к своей системе;
    Больно гордо будто оценить требуемый расход и набег (т.е. сколь м3/ч воды довольно использоваться, что метров в высоту, на каком этаже) в вашей системе трубопроводов, дабы выбрать правильную пример циркуляционного насоса;
    Предварительно покупкой любой помпы внимательно посмотрите зону покрытия сервисной узы продукта в стране;
    Посмотрите для энергетический комната насоса, чем он выше, тем больше денег вы сэкономите со временем;
    Присутствие необходимости проконсультируйтесь со специализированным установщиком ради всей вашей системы, чтобы быть спокойным и уверенным в отношении нужного вам продукта;
    Быть покупке насоса обратите забота, который в большинстве случаев параметр максимальный напор соответствует нулевому расходу и наоборот максимальный расход быть нулевом напоре. Вам должен посмотреть на соответствие потока/давления в таблице в соответствии с вашими потребностями;
    Присутствие покупке любого насоса поинтересуйтесь, сертифицирован ли он согласие BDS, другим международным стандартам и т. д. Отдельный дополнительный сертификат качества или покрываемый стандарт говорит о более стабильном и надежном продукте.

  36. Циркуляционный насос UP 15-14 B PM – Дания. Эти рециркуляционные насосы изготовлены из высококачественных материалов. Корпус изготовлен из латуни MS 68, а рабочее колесо – из легированной стали, EPDM, PPO, PTFE, Graphit. Циркуляционный насос однофазный, чрезвычайно экономичный, мощностью через 5 Вт до 8,5 Вт. Насос имеет одинарную проворство вращения ротора. Насос оснащен двигателем со сферическим плавающим ротором и встроенным рабочим колесом, подходящим для воды почти давлением. Посмотри какой циркуляционный насос выбрать для водоснабжения смотри на сайте nasoscirkulyacionnyi.ru как выбрать циркуляционный насос для системы отопления правильно в частном доме своими руками.
    Мы указываем примерные отношения расхода к напору : 0,45 м? / ч-0,8 м , 0,25 м? / ч-0,55 м или 0,05 м? / ч-1,1 м. Более подробную техническую информацию см. В разделе «Возможности» около описанием.
    Сей насос используется ради рециркуляции горячей воды для бытового потребления (ГВС) в водопроводных системах, частных домах, офисах, квартирах и т.п. Товар сертифицирован сообразно всем европейским требованиям, что само сообразно себе говорит о высоком качестве.
    Гарантийный срок составляет 2 возраст со дня покупки товара.
    Перед покупкой циркуляционного насоса проверьте, глотать ли в вашем комплекте какие-либо фитинги, воеже вы могли подключить его к своей системе;
    Очень гордо как оценить требуемый затрата и напор (т.е. что м3/ч воды довольно использоваться, сколько метров в высоту, для каком этаже) в вашей системе трубопроводов, воеже выбрать правильную образец циркуляционного насоса;
    Перед покупкой любой помпы внимательно посмотрите зону покрытия сервисной сети продукта в стране;
    Посмотрите на энергетический комната насоса, чем он выше, тем больше денег вы сэкономите со временем;
    Около необходимости проконсультируйтесь со специализированным установщиком чтобы всей вашей системы, дабы находиться спокойным и уверенным в отношении нужного вам продукта;
    Быть покупке насоса обратите внимание, который в большинстве случаев параметр максимальный набег соответствует нулевому расходу и обратно максимальный жертва присутствие нулевом напоре. Вам необходимо посмотреть на аналогия потока/давления в таблице в соответствии с вашими потребностями;
    При покупке любого насоса поинтересуйтесь, сертифицирован ли он согласно BDS, другим международным стандартам и т. д. Каждый дополнительный сертификат качества или покрываемый стандарт говорит о более стабильном и надежном продукте.

  37. Насос рециркуляции горячей воды дозволительно использовать чтобы немедленной подачи горячей воды в душевые и водопроводные краны, если это больше только надо, без потери воды в канализации в ожидании поступления горячей воды из бойлера. Коль у вас потреблять ванная аудитория и душ, расположенные для некотором расстоянии от бойлера, вы можете обнаружить, который вам нуждаться пить душ в ход 30 секунд разве более, прежде чем горячая вода из водонагревателя потечет по трубам и достигнет душа. Посмотри циркуляционный насос как выбрать для системы отопления частного дома смотри на сайте nasoscirkulyacionnyi.ru выбрать насос для отопления в частном доме как циркуляционный системы отопления.
    При установленном рециркуляционном насосе вода в трубопроводе горячей воды неустанно рециркулирует обратно в котел, а это значит, сколько она вовек горячая и готова к использованию. Существует несколько различных конструкций таких систем, однако систему мгновенной рециркуляции горячей воды, которую мы вам здесь покажем, достанет свободно установить в существующую систему.
    В разница через некоторых других систем, эта система не требует специального контура горячей воды и работает после циркуляционный насос, обыкновенный на котле, и обратный клапан, обыкновенный для самой дальней от котла раковине. Обратный клапан представляет собой термочувствительный клапан, какой направляет воду назад в бойлер, покамест он не довольно довольно теплым, а после отключается, если вода в трубопроводах горячей воды становится довольно теплой для использования. В результате вода в трубах с горячей водой всегда остается горячей, если вам это нужно, и вы николи не должны соединять воду в канализацию, ожидая, пока она нагреется.
    Хоть рециркуляционный насос потребляет небольшое сумма электроэнергии, это потребление энергии компенсируется экономией воды. В качестве функции энергосбережения большинство рециркуляционных насосов имеют встроенный таймер, что позволяет настроить насос для работу в течение дня, если вам, скорее только, понадобится горячая вода. Вы можете выключить насос на ночь, скажем, если горячая вода не нужна.
    Если вам когда-нибудь придется отключить подачу воды в дом, обязательно выключите насос, дабы не поджечь его. В насосе во срок работы должна циркулировать вода. Если произойдет сбой питания, таймер рециркуляционного насоса нуждаться будет рождать, дабы он запускался и останавливался в соответствующее время.

  38. Циркуляционный насос UP 15-14 B PM – Дания. Эти рециркуляционные насосы изготовлены из высококачественных материалов. Корпус изготовлен из латуни MS 68, а рабочее колесо – из легированной стали, EPDM, PPO, PTFE, Graphit. Циркуляционный насос однофазный, очень экономичный, мощностью через 5 Вт перед 8,5 Вт. Насос имеет одинарную быстрота вращения ротора. Насос оснащен двигателем со сферическим плавающим ротором и встроенным рабочим колесом, подходящим чтобы воды почти давлением. Посмотри формулы расчетов циркуляционных насосов системы отопления смотри на сайте nasoscirkulyacionnyi циркуляционные насосы какие выбрать.
    Мы указываем примерные отношения расхода к напору : 0,45 м? / ч-0,8 м , 0,25 м? / ч-0,55 м иначе 0,05 м? / ч-1,1 м. Более подробную техническую информацию см. В разделе «Возможности» перед описанием.
    Сей насос используется для рециркуляции горячей воды ради бытового потребления (ГВС) в водопроводных системах, частных домах, офисах, квартирах и т.п. Товар сертифицирован по всем европейским требованиям, который само по себе говорит о высоком качестве.
    Гарантийный срок составляет 2 возраст со дня покупки товара.
    Накануне покупкой циркуляционного насоса проверьте, есть ли в вашем комплекте какие-либо фитинги, воеже вы могли подключить его к своей системе;
    Донельзя гордо действительно оценить требуемый издержка и напор (т.е. сколь м3/ч воды будет использоваться, сколь метров в высоту, на каком этаже) в вашей системе трубопроводов, воеже выбрать правильную образец циркуляционного насоса;
    Накануне покупкой всякий помпы внимательно посмотрите зону покрытия сервисной путы продукта в стране;
    Посмотрите для энергетический комната насоса, чем он выше, тем больше денег вы сэкономите со временем;
    При необходимости проконсультируйтесь со специализированным установщиком для всей вашей системы, воеже являться спокойным и уверенным в отношении нужного вам продукта;
    Быть покупке насоса обратите забота, что в большинстве случаев параметр максимальный напор соответствует нулевому расходу и обратно максимальный затрата около нулевом напоре. Вам необходимо посмотреть на аналогия потока/давления в таблице в соответствии с вашими потребностями;
    Около покупке любого насоса поинтересуйтесь, сертифицирован ли он согласие BDS, другим международным стандартам и т. д. Отдельный дополнительный сертификат качества иначе покрываемый стандарт говорит о более стабильном и надежном продукте.

  39. Посмотрим правде в глаза – мы настолько зависимы через наших смартфонов, что готовы прожигать на них много денег и времени. Наша повседневная проживание полна уведомлений, наше дружба связано с эмодзи, мена забавными картинками, фотографиями, наши покупки находятся только в нескольких кликах. Вот почему мы неоднократно склонны выбрести ради рамки нашего бюджета и времени, дабы получить новую пример бренда, будь то просто из-за улучшенной камеры или большего дисплея. Впрочем ныне мы расскажем, как выбрать идеальный смартфон, не выходя после рамки вашего бюджета и не жертвуя своими предпочтениями. Смотри тут дешевые телефоны сенсорные андроид https://smartfonresurs.ru/xiaomi-mi-10t-pro-8-128-gb-5g-lunnoe-serebro-xiaomi/ сенсорные телефоны fly дешевые.
    На рынке смартфонов поглощать несколько основных факторов, о которых мы здесь расскажем. Первый посредник – это большая конкуренция посреди производителями телефонов. В результате цены падают, а возможности телефонов увеличиваются, поэтому одни модели ничем не хуже других, только сообразно более низкой цене. Второй посредник – стремительное развитие технологий. Новые смартфоны нередко появляются на рынке, что способствует быстрому падению цен на «как» устаревшие модели.
    В этой статье мы остановились на ценовом диапазоне. Необходимо провести очень глубокое исследование, воеже найти телефон стоимостью, из которого можно извлечь максимальную цену, которую мы заплатим. Быть выборе брендов смартфонов ради презентации, помимо цены, опять одним ключевым фактором, для что мы обращали уважение, является рыночная доза брендов в 2020 году.
    Общество Samsung была основана в 1938 году. Поручение компании: мы используем человеческие и технологические ресурсы компании ради создания товаров и услуг высочайшего качества, тем самым способствуя улучшению глобального состояния общества. Компания Samsung успешно выполнила свою миссию, и вот некоторые тому свидетельства. На 2020 год Samsung продала 80,2 миллиона устройств и, таким образом, занимает первое манеж по рыночной доле в 23% на 2020 год. Опричь того, их рыночная доза увеличилась на 2% по сравнению с предыдущим 2019 годом.
    В январе 2020 возраст компания Samsung выпустила для болгарский торжище новую образец среднего класса Samsung Galaxy A51. Мы предлагаем эту пример, потому сколько это стабильный телефон и удивительный выбор с точки зрения соотношения цены и качества. Для известный момент эту образец можно приобрести после скромные. С ней у вас будет бойкий телефон и потрясающая камера, а внутренней памяти телефона хватит, дабы собрать однако ваши книга в одном месте.

  40. Насос рециркуляции горячей воды дозволительно использовать для немедленной подачи горячей воды в душевые и водопроводные краны, если это больше только должен, без потери воды в канализации в ожидании поступления горячей воды из бойлера. Если у вас лакомиться ванная комната и душ, расположенные на некотором расстоянии через бойлера, вы можете обнаружить, сколько вам нуждаться пить душ в ход 30 секунд разве более, раньше чем горячая вода из водонагревателя потечет по трубам и достигнет душа. Посмотри циркуляционный насос для теплых полов как выбрать смотри на сайте nasoscirkulyacionnyi насос циркуляционный для частного дома как выбрать.
    Быть установленном рециркуляционном насосе вода в трубопроводе горячей воды безвыездно рециркулирует навыворот в котел, а это вероятно, что она вечно горячая и готова к использованию. Существует скольконибудь различных конструкций таких систем, но систему мгновенной рециркуляции горячей воды, которую мы вам здесь покажем, кончено свободно установить в существующую систему.
    В знак от некоторых других систем, эта способ не требует специального контура горячей воды и работает посредством циркуляционный насос, установленный на котле, и обратный клапан, обыкновенный на самой дальней от котла раковине. Обратный клапан представляет собой термочувствительный клапан, что направляет воду наоборот в бойлер, пока он не довольно достаточно теплым, а кроме отключается, если вода в трубопроводах горячей воды становится достаточно теплой чтобы использования. В результате вода в трубах с горячей водой издревле остается горячей, если вам это нужно, и вы никогда не должны соединять воду в канализацию, ожидая, покуда она нагреется.
    Что рециркуляционный насос потребляет небольшое сумма электроэнергии, это потребление энергии компенсируется экономией воды. В качестве функции энергосбережения большинство рециркуляционных насосов имеют встроенный таймер, какой позволяет настроить насос для работу в течение дня, если вам, скорее всего, понадобится горячая вода. Вы можете выключить насос на ночь, возьмем, когда горячая вода не нужна.
    Если вам когда-нибудь придется отключить подачу воды в хижина, обязательно выключите насос, дабы не поджечь его. В насосе во эпоха работы должна циркулировать вода. Буде произойдет сбой питания, таймер рециркуляционного насоса надо будет рождать, чтобы он запускался и останавливался в соответствующее время.

  41. Новые телефоны мощнее старых и соответственно дороже. Старые модели будут заниматься медленно, они могут даже не запустить приложение, которое вы хотите использовать.
    Эта положение отличается для двух основных операционных систем. Устройства Android со временем работают долго, в то время как устройства iOS не изменяют скорость даже затем нескольких лет использования.
    Обновления ОС также важны ради хорошей производительности и защиты личных данных. Смотри тут телефон сенсорный самсунг дешево https://smartfonresurs.ru/kruger-matz-move-8-mini-1-8/
    сенсорные телефоны дешевые на алиэкспресс.
    Неписаное обычай гласит, который смартфоны подлежат обновлению программного обеспечения безопасности в ход будто двух лет впоследствии выпуска модели. Особенность составляет конкретная серия – Google Pixel, устройства которой продолжают доставать обновления программного обеспечения даже после истечения срока производственной гарантии.
    Наш совет, если вы решили покупать старый смартфон, – сосредоточьтесь на моделях Apple, помощь программного обеспечения которых, кажется, длится дольше. Разумеется и сами устройства работают точный так же, даже впоследствии нескольких лет использования. Хоть флагманские модели с Android прекрасно справятся со своей задачей, купленные б/у.
    Имейте в виду, что единовластно через того, какую пример вы покупаете, в какой-то момент она довольно чрезвычайно старой, дабы адекватно побеждать даже с самыми простыми задачами, такими как серфинг в Интернете, использование программ чата, Viber, мессенджера Facebook и т. Д.
    Здесь отдельный обязан внимательно учитывать свои интересы и потребности, ведь всегда чаще в новых смартфонах, беспричинно через операционной системы, перевелись слота ради увеличения встроенной памяти. Облачные серверы предлагают приговор, однако следовать них взимается ежемесячная плата.
    Шестнадцать гигабайт внутренней памяти (16 ГБ) могут вместить почти 10 000 фотографий alias 4 000 песен. Обратите почтение, сколько эта память используется для ОС, обновлений и установленных приложений. Вы не можете использовать встроенную память для 100% для фотографий, музыки, видео.
    Смартфоны предлагают качественные фотографии, только все же ужинать разница от модели к модели и от бренда к бренду.
    В рекламе чаще всего сравнивают камеры для разных смартфонах с мегапикселями, но для качества фото или видео важнее ISO, яркость, съемка при слабом освещении, уступка бокового шума.
    Рекомендуется вживую попробовать снять камеру понравившейся модели в обычном магазине иначе сравнить фотографии, сделанные с помощью этого устройства и опубликованные в Интернете.

  42. Загодя или поздно всем придется покупать недавний смартфон. Причин много – батарея устройства стала быстрее разряжаться, некоторые приложения вылетают или пора подписывать новоиспеченный контракт. В результате в Болгарии ежегодно приобретаются сотни тысяч новых телефонов.
    Выбрать подходящее внушение не навсегда просто, и многим пользователям сложно опомниться в «море» новых смартфонов. Правда в часть, который не завсегда нуждаться платить огромную сумму, чтобы получить удовлетворительный телефон. Коль мы хотим выбрать наиболее выгодное и хорошее предложение для рынке, мы должны искать устройства, соответствующие определенным критериям. Смотри тут телефон сенсорный дешевые https://smartfonresurs.ru/samsung-galaxy-s20-128-gb-dve-sim-karty-samsung-2/ дешевые телефоны сенсорные недорого.
    Все чисто невольный отбор не ввек уместен. На рынке гибель смартфонов, которые хоть и хорошо выглядят на бумаге, только на самом деле страдают некачественными элементами для корпусе и имеют проблемы с контролем качества. По этой причине хорошо доставать из известных и любимых брендов в нашей стране.
    Ныне мы используем телефон в основном чтобы трех целей – ради серфинга в социальных сетях, чтобы чего нам нужен Интернет, чтобы разговоров и для фото- и видеосъемки. Чтобы любое новое устройство отлично справляется с первыми двумя задачами, присутствие съемке есть существенные различия.
    Воеже делать хорошие фотографии, в вашем смартфоне должна быть основная камера как минимум с 3 датчиками, и чем больше, тем лучше. Благодаря им вы сможете наслаждаться лучшими эффектами боке, учинять широкоугольные снимки и творить впечатляющие макро-фотографии.
    Столовать телефоны, в которых также ужинать особенный телеобъектив с хорошими возможностями масштабирования – оптического масштабирования и съемки удаленного объекта без потери качества.
    Большинство устройств премиум-класса оснащены дисплеями AMOLED, а не ЖК-матрицами IPS. Технология AMOLED гарантирует более широкий угол обзора, имеет значительно более широкую цветовую гамму, глубокий черный колер и отличную контрастность, поскольку отдельные пиксели могут скрываться исключены. Это помогает улучшить HDR, но также экономит заряд батареи.
    Добираемся до аккумулятора. Здесь нуждаться допытываться две багаж – аккумулятор большей емкости, годный трудиться без подзарядки два суток, и мощное зарядное строение для его быстрого «восстановления».
    Некоторый из более дешевых и лучших телефонов поставляются в комплекте с быстрой зарядкой. Благодаря ему вы можете весь зарядить особенный разряженный телефон прежде 50% всего после 30 минут. Полная зарядка тоже быстрая.
    Технология чрезвычайно полезна ради всех, кто работает. Коль заряд вашего телефона становится низким утром пред работой, достаточно подключить его к зарядному устройству во дата утренних дел. Быть отключении через сети заряда хватит на весь рабочий день.
    Разве вы собираетесь подкупать новое построение, рекомендуется поискать уклад с 8-ядерным процессором и минимум 4 ГБ оперативной памяти. Это гарантирует, который вы сможете извлекать частный телефон в ход более длительного времени, и он не будет «слабым» ради последних приложений путем год. Понятно, чем больше оперативной памяти и более сильный процессор у вашего телефона, тем дольше он довольно технологически актуальным.

  43. Как мне выбрать надлежащий смартфон? Это, казалось желание, элементарный задача, но он скрывает избыток подводных камней, которые следует учитывать.
    Вам нуждаться уточнить, что чтобы вас гордо в телефоне.
    Телефоны с ОГРОМНЫМ аккумулятором и прочностью:
    Выше смартфон с самой большой батареей емкостью 6050 мАч – Ulefone Power 2 (он также имеет некоторые из лучших характеристик – экран 5,5 дюйма, 8-ядерный процессор, 4 ГБ оперативной памяти, 64 ГБ встроенной памяти, 16-мегапиксельная суд).
    Следующий разночтение – с аккумулятором для 5050 мАч – DooGee BL5000 (у него тоже вовсю хорошие параметры – экран 5.5 „, 8-ядерный, 4 ГБ оперативной памяти, 64 ГБ встроенной памяти, 16-мегапиксельная ДВОЙНАЯ камера)
    У третьей модели лучшая цена.
    Они необычайно красивы и удобны благодаря большому экрану и при этом сохраняют меньшие размеры телефона. Если держишь телефон в руках, кажется, точно смотришь через него, ведь рамки со всех трех сторон минимальные. Смотри тут дешевые телефоны сенсорные в мегафоне https://smartfonresurs.ru/samsung-galaxy-note-10-256-gb-dve-sim-karty-samsung-2/ дешевый телефон сенсорный днс.
    В Doogee Go round безрамного смартфон (помимо того , что красиво, он наполнен новейшими технологиями – 5,5 – дюймовый экран, 8-ядерный процессор 2.6GHz, 4GB FORCE, память 64GB, 16MP Двойная комната, 2X оптический ZOOM)
    Коль вам нужен бюджетный смартфон (телефон, кто еще имеет дополнения операционной системы Android – Facebook, Viber, Skype, зрелище и приложения, с приличными параметрами и колоссально низкой ценой ниже 200 лв. )
    Лидером в этой категории является VKworld S3 с его невысокой ценой, у него миловидный дизайн RESTIVE, такой подобно Samsung galaxy S8, экран HD 5.5 дюймов, 4-ядерный процессор, комната 13MP, оперативная память 1GB.
    Не хуже второго варианта – DooGee X20 (он компактнее – экран 5 HD, ОЗУ 2 ГБ, 4-ядерный процессор, суд 8MP DUAL)
    Не худой третий вариант – VKworld F2 – (он более тесный – экран 5 HD, ОЗУ 2 ГБ, 4-ядерный процессор, камера 13 МП)
    Противоударный телефон – это разряд для людей, которым нужен прочный телефон, потому сколько этого требует делание либо хобби. Его нуждаться точный защитить через ударов, воды, пыли, грязи, вибраций и прочего.
    HOMTOM ZOJI Z7 (помимо того, сколько он благонадежный смартфон, он имеет вконец хорошие параметры, которыми в принципе не могут похвастаться ударопрочные телефоны. Это недостижимый выбор, сочетающий ударопрочность, мощное обстановка и в то же период дюже низкая курс Он может похвастаться Интернетом 4G, 4-ядерным процессором, 2 ГБ оперативной памяти, 5-дюймовым экраном, камерой 13 МП, датчиком отпечатков пальцев, аккумулятором для 3000 мАч .

  44. Посмотрим правде в глаза – мы настолько зависимы от наших смартфонов, который готовы прожигать для них воз денег и времени. Наша повседневная долгоденствие полна уведомлений, наше общение связано с эмодзи, мена забавными картинками, фотографиями, наши покупки находятся всего в нескольких кликах. Вот почему мы неоднократно склонны выходить за рамки нашего бюджета и времени, дабы получить новую модель бренда, будь то простой из-за улучшенной камеры тож большего дисплея. Однако ныне мы расскажем, наравне выбрать идеальный смартфон, не выходя изза рамки вашего бюджета и не жертвуя своими предпочтениями. Смотри тут самый дешевый сенсорный телефон челябинск https://smartfonresurs.ru/xiaomi-mi-10t-pro-8-128-gb-5g-lunnoe-serebro-xiaomi/ дешевые телефоны алкатель сенсорный.
    На рынке смартфонов употреблять изрядно основных факторов, о которых мы здесь расскажем. Главный фактор – это большая соперничество среди производителями телефонов. В результате цены падают, а возможности телефонов увеличиваются, следовательно одни модели ничем не хуже других, однако сообразно более низкой цене. Другой посредник – стремительное развитие технологий. Новые смартфоны неоднократно появляются для рынке, который способствует быстрому падению цен для «будто» устаревшие модели.
    В этой статье мы остановились для ценовом диапазоне. Необходимо провести очень глубокое испытание, дабы встречать телефон стоимостью, из которого позволительно извлечь максимальную цену, которую мы заплатим. При выборе брендов смартфонов чтобы презентации, кроме цены, еще одним ключевым фактором, на который мы обращали почтение, является рыночная доля брендов в 2020 году.
    Группа Samsung была основана в 1938 году. Задача компании: мы используем человеческие и технологические ресурсы компании чтобы создания товаров и услуг высочайшего качества, тем самым способствуя улучшению глобального состояния общества. Общество Samsung успешно выполнила свою миссию, и вот некоторые тому свидетельства. На 2020 год Samsung продала 80,2 миллиона устройств и, таким образом, занимает первое столица по рыночной доле в 23% для 2020 год. Опричь того, их рыночная судьба увеличилась на 2% сообразно сравнению с предыдущим 2019 годом.
    В январе 2020 года общество Samsung выпустила для болгарский торжище новую модель среднего класса Samsung Galaxy A51. Мы предлагаем эту форма, потому который это стабильный телефон и чудный подбор с точки зрения соотношения цены и качества. На известный момент эту образец дозволительно приобрести ради скромные. С ней у вас будет рьяный телефон и потрясающая комната, а внутренней памяти телефона хватит, дабы собрать все ваши книга в одном месте.

  45. Смартфоны – самые личные, полезные и используемые устройства в современной повседневной жизни. Бывают исключения, но обычно мы покупаем телефон, которым пользуемся два, а коекогда и больше года, следовательно нужно скрываться осторожным при выборе. Преимущественно это актуально чтобы лизинга устройств путем операторов мобильной связи. Уродливый запас может означать, что нам осталось то, что нас не устраивает, и надолго. Конечно, мы можем продать его и рефинансировать в другом устройстве, только это дополнительные проблемы, которых следует избегать.
    Сегодня на рынке противопоказуется отказываться одно – десятки моделей, мобильный интернет, бесчисленное мера приложений. Все это сильно, но делает подбор опять сложнее. Цель здесь не в том, воеже указать на форма и сказать: «Вот она. Это он! » Мысль состоит скорее в книга, дабы выстроить какое-то направление и общее мысль о книга, чего можно надеяться от рынка. Якобы и все остальное, синод – вещь относительная, которая здорово зависит от личных предпочтений, но тем не менее – это хорошее пролог .
    Покупка важна, однако это последнее выходка, перед ней глотать над чем подумать. С одной стороны, если у вас теперь полдничать смартфон, вероятность того, который вы связаны контрактом с оператором, высока. Приостановление такого контракта стоит дорогой, а сообразно правилам операторов – совершенно бессмысленно (оплатить безвыездно ежемесячные платежи, которые остаются накануне конца контракта). Это нормально, поскольку понятие «контракта» заключается в часть, дабы возбранять клиентов у одного оператора, воеже они не сбегали к другому. Смотри тут сенсорные телефоны по дешево https://smartfonresurs.ru/samsung-galaxy-z-flip-5g-sm-f707-seryj-samsung/ дешевые телефоны сенсорные хорошие. С противоположный стороны, вам может слишком понравиться этот конкретный оператор и вы не захотите его менять, вся семья может целить его услугами или ваши визитки могут простой составлять с ним.В лучшем случае истекающий договор – в нужном месте в нужное время.
    Эксклюзивные телефоны – большая редкость. Все флагманы предлагаются всеми тремя нашими операторами. Могут пребывать небольшие отличия (примерно, iPhone , которого нет для Vivacom, или серия Nexus , премьера которой снова не состоялась для Globul), однако в целом пастель общая. Точно известно, у нас три мобильных оператора . Они гурьбой уже столько лет, сколько здесь перевелись ничего нового. Говоря о смартфоне, вельми важно уделять особое уважение тарифным планам.(это, конечно, ежели вы решите побеждать телефон с подпиской), которые предлагают «безлимитный» мобильный интернет. Начинать у него уплетать ограничение, однако не в мегабайтах, а в скорости. Операторы предлагают определенные мегабайты, которые пользователь может использовать на максимальной скорости, а по истечении их срока – быстрота падает прилично. Вот почему гордо точно учитывать, ради чего вам понадобится этот Интернет. Существует также вариант, при котором вы не делаете ставку на такую ??подписку, поскольку вы будете пользоваться телефон единственно с Wi-Fi, но, по нашему мнению, сей путь теряет большую пай идеи, которая встроена в эти интеллектуальные устройства (с постоянным доступом в Интернет). вы сможете извлекать постоянно приложения ради бесплатных текстовых сообщений либо звонков, который может свободно привести к резкому сокращению вашего общего ежемесячного счета).

  46. Циркуляционный насос UP 15-14 B PM – Дания. Эти рециркуляционные насосы изготовлены из высококачественных материалов. Корпус изготовлен из латуни MS 68, а рабочее колесо – из легированной стали, EPDM, PPO, PTFE, Graphit. Циркуляционный насос однофазный, чрезвычайно экономичный, мощностью от 5 Вт предварительно 8,5 Вт. Насос имеет одинарную резвость вращения ротора. Насос оснащен двигателем со сферическим плавающим ротором и встроенным рабочим колесом, подходящим ради воды под давлением. Посмотри насос циркуляционный для отопления рейтинг какой выбрать частного дома смотри на сайте nasoscirkulyacionnyi.ru насос циркуляционный для отопления как выбрать цена.
    Мы указываем примерные отношения расхода к напору : 0,45 м? / ч-0,8 м , 0,25 м? / ч-0,55 м или 0,05 м? / ч-1,1 м. Более подробную техническую информацию см. В разделе «Возможности» около описанием.
    Этот насос используется ради рециркуляции горячей воды ради бытового потребления (ГВС) в водопроводных системах, частных домах, офисах, квартирах и т.п. Товар сертифицирован сообразно всем европейским требованиям, который само сообразно себе говорит о высоком качестве.
    Гарантийный срок составляет 2 года со дня покупки товара.
    Перед покупкой циркуляционного насоса проверьте, трескать ли в вашем комплекте какие-либо фитинги, дабы вы могли подключить его к своей системе;
    Больно важно как оценить требуемый издержка и набег (т.е. что м3/ч воды будет использоваться, сколько метров в высоту, на каком этаже) в вашей системе трубопроводов, воеже выбрать правильную модель циркуляционного насоса;
    Предварительно покупкой любой помпы внимательно посмотрите зону покрытия сервисной узы продукта в стране;
    Посмотрите на энергетический комната насоса, чем он выше, тем больше денег вы сэкономите со временем;
    Быть необходимости проконсультируйтесь со специализированным установщиком ради всей вашей системы, для являться спокойным и уверенным в отношении нужного вам продукта;
    При покупке насоса обратите почтение, который в большинстве случаев параметр максимальный напор соответствует нулевому расходу и превратно максимальный расход присутствие нулевом напоре. Вам должен посмотреть на соответствие потока/давления в таблице в соответствии с вашими потребностями;
    Быть покупке любого насоса поинтересуйтесь, сертифицирован ли он согласно BDS, другим международным стандартам и т. д. Отдельный дополнительный сертификат качества разве покрываемый стандарт говорит о более стабильном и надежном продукте.

  47. Как выбрать смартфон? Все основную долю рынка в 53,9% занимают три крупнейших производителя – Samsung (21,8%), Huawei (17,6%) и Apple (14,5%). Это сужает выбор людей, доверяющих проверенному качеству производителя мобильных телефонов. Смотри тут дешевые телефоны сенсорные за 5000 https://smartfonresurs.ru/myphone-hammer-force-myphone/ дешевые телефоны сенсорные с большим экраном.
    Что в начале 2020 г. На мировом рынке смартфонов наблюдается спад , мы можем объяснить это внешними факторами, которые не окажут постоянного влияния для действие и продажи. Даже желание такова, сколько потребители безвыездно больше зависят от своих смартфонов, и выравнивание рыночных долей ведущих производителей свидетельствует о прогрессивном улучшении мобильных телефонов, которые уже стали неотъемлемой и необходимой частью нашей жизни.
    Туз посредник, разделяющий смартфоны – это операционная система.
    В настоящее время двумя основными являются Android, разработанный Google и iOS, разработанный Apple. А затем того, вроде правительство США запретило американским компаниям купить сетевое оборудование у Huawei и Google предлагать Android Huawei, последний объявил о разработке собственной операционной системы для мобильных устройств, которая сделает их автономными и, знать, увеличит долю рынка. система становится фактом.
    Ежели у вас уже столовать опыт работы с компьютером иначе планшетом почти управлением одной из операционных систем, и вы удовлетворены услугами и тем, вроде ими управляют, первый видоизменение – купить мобильный телефон с той же операционной системой.
    Гордо отметить, сколько наиболее многократно используемые приложения, такие только почтовый клиент, GPS-навигация, облачные сервисы и т. Д. доступны для обеих платформах, сиречь вы можете встречать альтернативное приложение, которое предоставляет те же услуги, который и исходное, недоступное ради выбранной вами платформы.
    При покупке приложений, приложений и смене смартфона платная лицензия является вашей собственностью, и вам простой надо загрузить добавление на свое новость устройство. Это предлагается обеими операционными системами.
    Пробегать статьи, книги и электронные письма для больших экранах относительно легко.
    Однако большой экран разряжает аккумулятор мобильного устройства. Пятьдесят процентов потребляемой энергии используется дисплеем.
    Стоимость не должна водиться проблемой, отдельный деятель предлагает мобильные устройства с большими экранами в низком и среднем ценовом диапазоне, сколько позволяет всем пользователям брать выгоду.

  48. iOS – это операционная порядок, используемая всего продуктами Apple. Он известен простотой использования, безопасностью и быстрой интеграцией с другими устройствами Apple.
    Android, с другой стороны, предполагает интеграцию сервисов Google. Устройства, которые его используют, обычно дешевле.
    Выше вече – по возможности проверить частный выбор места в магазине. Беспричинно вы сможете почувствовать интерфейс и получить мысль о некоторых основных функциях.
    Телефоны IOS (iPhone) обычно позиционируются в самом высоком ценовом диапазоне. Между производителей телефонов в целом Apple и Samsung обычно являются одними из самых дорогих, в то дата только HTC, LG и Motorola производят более дешевые модели. Смотри тут телефоны дешевые но хорошие сенсорные smartfonresurs дешевые телефоны сенсорные.
    Если у вас уже обедать планшет тож компьютер, проще всего будет выбрать телефон, совместимый с его услугами и программным обеспечением. Впрочем учтите, что любой телефон может подключаться и сидеть практически с всякий компьютерной операционной системой.
    Каждая операционная способ имеет свои собственные функции, в то период только основные, такие якобы электронная почта, просмотр веб-страниц и карты, доступны для всех устройствах.
    iOS / iPhone имеет эксклюзивные функции, такие якобы Siri, сканирование отпечатков пальцев, чат FaceTime и помощь iCloud.
    В Android есть Google Promptly, настраиваемый виджет для главном экране, что позволяет устанавливать сторонние приложения (то глотать вы можете загружать приложения из Интернета и устанавливать их вне экосистемы Have fun Hoard). Большинство современных телефонов Android также имеют датчики отпечатков пальцев, облачное хранилище для фотографий и поддерживают использование Google Диска для документов.
    Некоторый популярные приложения (примерно, Google Maps, MS Office и Apple Music) доступны во всех операционных системах, только теснить некоторые приложения (примем, iMessage, Facetime и Google Age), которые предназначены только чтобы соответствующей платформы. Проверьте магазин приложений, связанный с каждой опцией, воеже убедиться, что нужные вам приложения доступны (Apple, Google Margin).
    В общем, когда популярное добавление недоступно в операционной системе конкурента, высока вероятность того, что существует альтернативное добавление, которое функционально бесконечно похоже.
    Величина экрана измеряется сообразно диагонали от угла предварительно угла. В конце концов, величина экрана – это урок предпочтений. Телефоны с меньшим экраном лучше умещаются в кармане и часто дешевле. Если вы планируете воззриться избыток видео, могут водиться предпочтительны дисплеи большего размера.
    iPhone предлагает серию SE для компактных телефонов и серию Added чтобы сверхбольших экранов.
    Телефоны Android доступны в широком диапазоне размеров: пожирать модели меньшего бюджета, такие словно Moto G alias Galaxy S Mini, модели среднего уровня, такие якобы серии Galaxy S или HTC One, и большие размеры, такие якобы Galaxy Note тож Nexus 6P.

  49. Насос рециркуляции горячей воды позволительно пользоваться для немедленной подачи горячей воды в душевые и водопроводные краны, когда это больше всего необходимо, без потери воды в канализации в ожидании поступления горячей воды из бойлера. Коли у вас столоваться ванная комната и душ, расположенные на некотором расстоянии от бойлера, вы можете обнаружить, который вам нужно принимать душ в ход 30 секунд alias более, накануне чем горячая вода из водонагревателя потечет по трубам и достигнет душа. Посмотри расчет формулы циркуляционного насоса смотри на сайте nasoscirkulyacionnyi.ru ибп для насоса отопления какой выбрать циркуляционного.
    Около установленном рециркуляционном насосе вода в трубопроводе горячей воды все рециркулирует навыворот в котел, а это вероятно, сколько она вовек горячая и готова к использованию. Существует изрядно различных конструкций таких систем, только систему мгновенной рециркуляции горячей воды, которую мы вам здесь покажем, достанет свободно установить в существующую систему.
    В разница от некоторых других систем, эта учение не требует специального контура горячей воды и работает чрез циркуляционный насос, установленный для котле, и обратный клапан, установленный на самой дальней от котла раковине. Обратный клапан представляет собой термочувствительный клапан, что направляет воду вспять в бойлер, временно он не довольно довольно теплым, а после отключается, когда вода в трубопроводах горячей воды становится довольно теплой ради использования. В результате вода в трубах с горячей водой вечно остается горячей, когда вам это нужно, и вы николи не должны соединять воду в канализацию, ожидая, временно она нагреется.
    Чтобы рециркуляционный насос потребляет небольшое количество электроэнергии, это потребление энергии компенсируется экономией воды. В качестве функции энергосбережения большинство рециркуляционных насосов имеют встроенный таймер, что позволяет настроить насос для работу в ход дня, когда вам, скорее только, понадобится горячая вода. Вы можете выключить насос для ночь, возьмем, когда горячая вода не нужна.
    Ежели вам когда-нибудь придется отключить подачу воды в лачуга, обязательно выключите насос, дабы не поджечь его. В насосе во срок работы должна циркулировать вода. Если произойдет сбой питания, таймер рециркуляционного насоса необходимо довольно сбросить, для он запускался и останавливался в соответствующее время.

  50. Новые телефоны мощнее старых и соответственно дороже. Старые модели будут работать медленно, они могут даже не запустить приложение, которое вы хотите использовать.
    Эта положение отличается для двух основных операционных систем. Устройства Android со временем работают долго, в то срок наподобие устройства iOS не изменяют быстрота даже затем нескольких лет использования.
    Обновления ОС также важны чтобы хорошей производительности и защиты личных данных. Смотри тут самые дешевые сенсорные телефоны днс https://smartfonresurs.ru/kruger-matz-move-8-mini-1-8/
    самая дешевая телефон сенсорный.
    Неписаное обыкновенный гласит, который смартфоны подлежат обновлению программного обеспечения безопасности в ход примерно двух лет после выпуска модели. Исключение составляет конкретная разряд – Google Pixel, устройства которой продолжают доставать обновления программного обеспечения даже после истечения срока производственной гарантии.
    Наш внушение, ежели вы решили подкупать старый смартфон, – сосредоточьтесь на моделях Apple, поддержка программного обеспечения которых, кажется, длится дольше. Разумеется и сами устройства работают действительно беспричинно же, даже после нескольких лет использования. Хотя флагманские модели с Android прекрасно справятся со своей задачей, купленные б/у.
    Имейте в виду, что единовластно от того, какую пример вы покупаете, в какой-то момент она будет чересчур старой, чтобы адекватно узнавать даже с самыми простыми задачами, такими наподобие серфинг в Интернете, использование программ чата, Viber, мессенджера Facebook и т. Д.
    Здесь отдельный вынужден внимательно учитывать свои интересы и потребности, ведь всегда чаще в новых смартфонах, независимо через операционной системы, вышли слота чтобы увеличения встроенной памяти. Облачные серверы предлагают приговор, но после них взимается ежемесячная плата.
    Шестнадцать гигабайт внутренней памяти (16 ГБ) могут вместить близ 10 000 фотографий alias 4 000 песен. Обратите забота, сколько эта память используется ради ОС, обновлений и установленных приложений. Вы не можете использовать встроенную память на 100% ради фотографий, музыки, видео.
    Смартфоны предлагают качественные фотографии, однако всетаки же есть разница через модели к модели и через бренда к бренду.
    В рекламе чаще только сравнивают камеры на разных смартфонах с мегапикселями, но для качества фото либо видео важнее ISO, яркость, съемка около слабом освещении, скидка бокового шума.
    Рекомендуется вживую рисковать снять камеру понравившейся модели в обычном магазине иначе сравнить фотографии, сделанные с через этого устройства и опубликованные в Интернете.

  51. Якобы выбрать лучший смартфон ради нас? С развитием технологий всетаки производители стремятся потчевать нам более умные и дешевые устройства. С одной стороны, это хорошо чтобы потребителей – базар довольно разнообразным и динамичным, и каждому найдется подходящее решение. Только при большом количестве предложений моментально возникает закономерный урок – что выбрать? Здесь большое состав играет плохую шутку, заставляя человека оглядываться и сигать через модели к модели. Смотри тут большой сенсорный телефон дешево https://smartfonresurs.ru/apple-iphone-12-mini-64-gb-dve-sim-karty-apple-2/ сенсорный телефон samsung самый дешевый.
    Воеже помочь тем, кто не в курсе последних моделей либо не обладает достаточными знаниями в этой области, мы в Plasico IT Superstore представим вам статью, содержащую рекомендации и советы, которые помогут вам сориентироваться в книга, который вы ищете, в одном смартфоне и направит вас к наиболее подходящим моделям.
    Поскольку собрание, которую вы дадите ради «пластиковый кирпич», существенна, мы разделим диапазон цен на несколько. В первую из них входят самые дешевые устройства, которые подходят чтобы основных функций – прослушивание музыки, испытание веб-страниц в Интернете и Facebook, отправка / получение сообщений через специализированные приложения – Viber, What’s Up, Messenger. Весь устройства имеют минимальный величина оперативной памяти, базовый двух- alias четырехъядерный процессор, заднюю камеру с приличным разрешением и слот ради карты памяти. В большинстве случаев вы можете установить две SIM-карты, которые не будут активны одновременно – если одна находится в состоянии разговора, другая довольно отключена от силок или довольно сигнализировать о занятости. Лучшее суждение в этом сегменте – Lenovo A Extra (A1010) .
    Повышение цены приводит к невыносимо высокому скачку параметров. Процессор, оперативная память и дисплей были обновлены, и теперь они могут легко вонзать несколько приложений зараз, а также играть в средние и тяжелые игры. За первое поместье борются два варианта – HUAWEI P8 Lite и Lenovo K6 . В матче преобладает китайский деятель (гм, какой?) – Lenovo. Который отличает его через прямого конкурента, так это предпочтительный дисплей, более новая операционная система и более быстрый процессор. Вы также можете встречать с ним сканер отпечатков пальцев;
    Будущий аллюр дает нам возможность прикоснуться к высококачественным смартфонам с большим объемом оперативной памяти, быстрыми 4- и 8-ядерными процессорами, дисплеем FullHD и поистине хорошей камерой. В этом классе мы покажем вам четыре совет – Motorola Moto G5 And , Motorola Moto X Style , Meizu M3 Note и Lenovo K5 Note . Каждой из этих моделей удается блистать вещами, которые мы перечислим в порядке номеров:
    Новейшая операционная способ Android 7.0, FullHD IPS-дисплей и быстрая конфигурация, четырехъядерный процессор с тактовой частотой 2,0 ГГц + 3 ГБ оперативной памяти;
    Quad HD IPS-дисплей, порывистый 6-ядерный процессор с 3 ГБ оперативной памяти, исключительно хорошая задняя суд 21 МП и предохранение через пыли и водяных брызг;
    FullHD IPS-дисплей с эксклюзивными цветами, 8-ядерный процессор с 3 ГБ оперативной памяти и значительный аккумулятор;
    FullHD IPS-дисплей, 8-ядерный процессор, вовсю хорошая суд на 13 МП и исключительное соответствие достоинство / полет;

  52. Наравне мне выбрать кстати смартфон? Это, казалось бы, незатейливый вопрос, но он скрывает много подводных камней, которые следует учитывать.
    Вам надо уточнить, который ради вас гордо в телефоне.
    Телефоны с ОГРОМНЫМ аккумулятором и прочностью:
    Выше смартфон с самой исполинский батареей емкостью 6050 мАч – Ulefone Power 2 (он также имеет некоторые из лучших характеристик – экран 5,5 дюйма, 8-ядерный процессор, 4 ГБ оперативной памяти, 64 ГБ встроенной памяти, 16-мегапиксельная комната).
    Дальнейший разночтение – с аккумулятором на 5050 мАч – DooGee BL5000 (у него тоже вовсю хорошие параметры – экран 5.5 „, 8-ядерный, 4 ГБ оперативной памяти, 64 ГБ встроенной памяти, 16-мегапиксельная ДВОЙНАЯ суд)
    У третьей модели лучшая цена.
    Они необычайно красивы и удобны благодаря большому экрану и при этом сохраняют меньшие размеры телефона. Если держишь телефон в руках, кажется, будто смотришь через него, ведь рамки со всех трех сторон минимальные. Смотри тут телефон сенсорный дешево в интернет магазине https://smartfonresurs.ru/samsung-galaxy-note-10-256-gb-dve-sim-karty-samsung-2/ дешевые сенсорные телефоны от 1000.
    В Doogee Distribution безрамного смартфон (кроме того , сколько красиво, он наполнен новейшими технологиями – 5,5 – дюймовый экран, 8-ядерный процессор 2.6GHz, 4GB FORCE, память 64GB, 16MP Двойная комната, 2X оптический ZOOM)
    Буде вам нужен бюджетный смартфон (телефон, кто еще имеет дополнения операционной системы Android – Facebook, Viber, Skype, игры и приложения, с приличными параметрами и ужасно низкой ценой ниже 200 лв. )
    Лидером в этой категории является VKworld S3 с его невысокой ценой, у него пригожий дизайн ITCHY, такой подобно Samsung galaxy S8, экран HD 5.5 дюймов, 4-ядерный процессор, комната 13MP, оперативная память 1GB.
    Не хуже второго варианта – DooGee X20 (он компактнее – экран 5 HD, ОЗУ 2 ГБ, 4-ядерный процессор, камера 8MP DUAL)
    Не худой третий видоизменение – VKworld F2 – (он более компактный – экран 5 HD, ОЗУ 2 ГБ, 4-ядерный процессор, камера 13 МП)
    Противоударный телефон – это категория чтобы людей, которым нужен прочный телефон, потому который этого требует подвиг либо хобби. Его нуждаться дополнительно защитить от ударов, воды, пыли, грязи, вибраций и прочего.
    HOMTOM ZOJI Z7 (помимо того, который он верный смартфон, он имеет бесконечно хорошие параметры, которыми в принципе не могут похвастаться ударопрочные телефоны. Это совершенный запас, сочетающий ударопрочность, мощное оборудование и в то же эпоха дюже низкая курс Он может похвастаться Интернетом 4G, 4-ядерным процессором, 2 ГБ оперативной памяти, 5-дюймовым экраном, камерой 13 МП, датчиком отпечатков пальцев, аккумулятором для 3000 мАч .

  53. Насос рециркуляции горячей воды дозволительно использовать чтобы немедленной подачи горячей воды в душевые и водопроводные краны, когда это больше только нуждаться, без потери воды в канализации в ожидании поступления горячей воды из бойлера. Коли у вас есть ванная комната и душ, расположенные для некотором расстоянии через бойлера, вы можете обнаружить, сколько вам нужно пить душ в течение 30 секунд разве более, накануне чем горячая вода из водонагревателя потечет сообразно трубам и достигнет душа. Посмотри как правильно выбрать циркуляционные насосы смотри на сайте nasoscirkulyacionnyi формула расчета циркуляционного насоса.
    Около установленном рециркуляционном насосе вода в трубопроводе горячей воды неустанно рециркулирует обратно в котел, а это вероятно, который она вечно горячая и готова к использованию. Существует изрядно различных конструкций таких систем, но систему мгновенной рециркуляции горячей воды, которую мы вам здесь покажем, станет легко установить в существующую систему.
    В разница от некоторых других систем, эта учение не требует специального контура горячей воды и работает после циркуляционный насос, установленный для котле, и обратный клапан, обыкновенный для самой дальней через котла раковине. Обратный клапан представляет собой термочувствительный клапан, который направляет воду вспять в бойлер, покамест он не довольно довольно теплым, а после отключается, если вода в трубопроводах горячей воды становится довольно теплой ради использования. В результате вода в трубах с горячей водой вечно остается горячей, если вам это нуждаться, и вы никогда не должны соединять воду в канализацию, ожидая, покамест она нагреется.
    Хоть рециркуляционный насос потребляет небольшое число электроэнергии, это потребление энергии компенсируется экономией воды. В качестве функции энергосбережения большинство рециркуляционных насосов имеют встроенный таймер, что позволяет настроить насос на работу в ход дня, когда вам, скорее всего, понадобится горячая вода. Вы можете выключить насос для ночь, например, когда горячая вода не нужна.
    Буде вам когда-нибудь придется отключить подачу воды в лачуга, непременно выключите насос, воеже не поджечь его. В насосе во срок работы должна циркулировать вода. Коли произойдет сбой питания, таймер рециркуляционного насоса надо довольно рождать, чтобы он запускался и останавливался в соответствующее время.

  59. Телефон с двумя SIM-картами
    Телефон с двумя SIM-картами — это мобильный телефон, обычно смартфон, с возможностью использования двух SIM- карт модуля идентификации абонента.
    SIM-карта — это смарт-карта, для которой хранятся причина о владельце, включая идентификационные причина и предпочтения пользователя, местоположение и номер телефона, данные авторизации в путы, личные ключи безопасности, списки контактов и сохраненные текстовые сообщения. Воеже передать причина на новый телефон, пользователю достаточно вынуть SIM-карту из одного телефона и вмешиваться ее в другой.
    Телефоны с двумя SIM-картами используются ради ряда целей, включая следующие:
    Два человека могут иметь одним телефоном, каждый со своим номером телефона и данными, хранящимися для разных SIM-картах. Смотри тут самые дешевые телефоны самсунг сенсорные https://smartfonresurs.ru/xiaomi-mi-note-10-lite-64-gb-dve-sim-karty-xiaomi/ телефоны дешевые сенсорные андроид.
    В среде BYOD сотрудники могут быть свои личные номера и данные одиноко от рабочих.
    Люди могут пользоваться работник и собственный номера на одном телефоне, а не совмещать нужда с отдельными телефонными трубками.
    Путешественники могут приобрести местную SIM-карту, дабы избежать платы за роуминг, оставаясь присутствие этом доступными сообразно своему обычному номеру.
    Вы все прекрасно знаете, сколько две SIM-карты — главная исключение наших телефонов. С самого начала Wiko оборудовала отдельный из своих телефонов функцией двух SIM-карт.
    Только что такое двойная SIM-карта и наравне она работает?
    Функция двух SIM-карт позволяет пользователю враз использовать две разные услуги без необходимости использования двух отдельных телефонов. Возьмем, единодержавно и тот же телефон дозволительно использовать чтобы личных и профессиональных целей с разными номерами и разными счетами либо ради путешествий с конкретной SIM-картой для страны назначения.
    Благодаря этой функции двух SIM-карт с вами позволительно связаться по обоим номерам с одного телефона.
    Существует изрядно различных типов двойных SIM-карт, предлагающих различные функции. Наши телефоны Wiko оснащены SIM DUAL STANDBY — обе SIM-карты могут принимать звонки. Всетаки присутствие подключении вызова для одну SIM-карту другая перестает попадаться активной и безвыездно входящие вызовы перенаправляются для голосовую почту. До сих пор весь наши модели были оснащены мини-слотами (обычными) SIM-картами.
    DARKMOON будет пользоваться слот ради мини-SIM и слот для микро-SIM, а DARKFULL — два слота чтобы микро-SIM.
    Самые ранние телефоны с двумя SIM-картами были просто адаптерами (псевдо-двойными иначе пассивными), сколько означало, который, хотя они могли таскать две карты, в любой момент времени работала единственно одна, и вам приходилось переключаться между ними быть необходимости. Чуть более развитая образец — Dual Sim Stalwart, где обе карты работают одновременно, однако присутствие поступлении вызова на одну карту другая деактивируется для эпоха разговора.
    Телефоны Dual Sim On the go (DSA) ныне более распространены: они способны принимать вызовы на обе SIM-карты, а более продвинутые модели позволяют пользователям брать вызов для оба номера сразу, который называется Dual Label иначе Dual Active.
    Некоторые модели, имея два слота, не дают одинаковой функциональности обоим: возьмем, главный слот чтобы карты обеспечивает борзый мобильный интернет 3G либо 4G, а дополнительный слот может являться ограничен более медленным 2G.

  60. Преимущества телефона с двумя SIM-картами
    Первое явное превосходство использования устройства с двумя SIM-картами заключается в книга, который оно позволяет пользователю разделить приманка личные и деловые связи. Это бонус во многих отношениях, включая возможность разделять рабочие и личные контакты. Смотри тут какой самый дешевый телефон сенсорный телефон https://smartfonresurs.ru/ulefone-armor-3w-64-gb-dve-sim-karty-ulefone/ лучший дешевый сенсорный телефон.
    Это также устраняет нужда носить с собой скольконибудь устройств.
    Паки один общеизвестный бонус заключается в том, что пользователю больше не нужно менять SIM-карты, чтобы пользоваться их. Доступ среди каждым из них дозволительно свободно активировать тож отключить с через нескольких простых нажатий кнопок.
    Помимо того, вы сможете свободно просматривать каждое выделка соответствующих телефонных номеров для устройстве. Это позволяет упростить отслеживание профессиональных финансов.
    С устройствами RugGear™ с двумя SIM-картами вы получаете не один перечисленные выше преимущества, но и защиту через пыли и воды IP-68, сертификацию MIL-STD 810G и длительное время автономной работы. Эти объединенные аспекты обеспечивают надежное и производительное устройство. Чтобы удовлетворить эти потребности, RugGear предлагает порядком устройств. Для смартфона RG655 предлагает всетаки вышеперечисленное, а также большую внутреннюю память и специальную кнопку PTT. Если вам больше подходит функциональный телефон, RG160 предоставит вам безвыездно необходимое в удобном для использования формате. Чтобы испытывать больше, вы можете посетить наши страницы продуктов.
    Сколько такое телефоны с двумя SIM-картами?
    Телефоны с двумя SIM-картами — это телефоны, которые содержат две физические SIM-карты или одну физическую SIM-карту и одну встроенную SIM-карту. Человек используют телефоны с двумя SIM-картами, как положение, сообразно следующим трем причинам:
    Для разделить личные и деловые звонки: некоторые человек могут захотеть разделить работу и дом. Они используют нераздельно часть телефона для связи с коллегами по рабочим вопросам, а непохожий номер телефона используется чтобы связи с членами семьи и друзьями.
    Для большего покрытия: в местах, где чтобы звонков промеж клиентами одного и того же провайдера действуют более низкие цены, где в одной путы может не ухватывать полного покрытия. Коли у вас наедаться телефон с двумя SIM-картами, вы можете получить больше покрытия, воеже успешно общаться с другими людьми.
    Чтобы экономии денег в путешествии: с телефоном с двумя SIM-картами вы можете сэкономить капитал на международной плате изза передачу данных во эра путешествия. Вы можете пользоваться свою собственную SIM-карту в одном слоте и пользоваться предоплаченную SIM-карту из страны назначения во втором. Это позволит вам избежать огромных сборов за международный роуминг данных, однако быть этом сохранить доступ к вашему номеру телефона изза границей.
    Для резервного копирования: с телефоном с двумя SIM-картами вы можете использовать одну SIM-карту в обычном режиме, а другую резервировать причина первой SIM-карты. Это означает большее хранилище и резервное копирование.
    Другими словами, по вышеуказанным 4 основным причинам телефоны с двумя SIM-картами становятся популярными, и некоторый люди владеют телефонами с двумя SIM-картами. Вы можете замечать, который многие устройства, использующие две SIM-карты, также были разработаны и выпущены. Тогда вы хотите свет, чистый работают телефоны с двумя SIM-картами?

  61. Будто вы можете пользоваться четыре или пять SIM-карт в своем iPhone иначе Android-смартфоне
    Чтобы теперь многие высококлассные смартфоны поддерживают более одной SIM-карты, подчас вам нуждаться больше. Намного больше.
    Чтобы людей, которые хотят разделить свою работу и домашнюю общежитие либо облако путешествуют сообразно разным странам, возможность переключения посреди SIM-картами в вашем смартфоне имеет большой смысл. И хоть большинство смартфонов высокого класса сейчас поддерживают порядком SIM-карт, вам может нуждаться больше. Иначе, вероятно, вы используете ветхий смартфон, в котором лопать исключительно один слот чтобы SIM-карты. Смотри тут телефона дешевые сенсорные телефоны https://smartfonresurs.ru/xiaomi-mi-10-5g-128-gb-odna-sim-karta-xiaomi/ дешевый телефон сенсорный за 3000.
    Вытаскивание лотка чтобы SIM-карты и пьеса с жестяными SIM-картами — это рецепт потери SIM-карты иначе, который вдобавок хуже, лотка. Утеря лотка чтобы SIM-карты — это настоящая головная боль, скажу я вам!
    Избавьте себя через хлопот и приобретите орудие, позволяющий использовать изрядно SIM-карт.
    SIMore уже много лет производит адаптеры чтобы SIM-карт, и они продолжают исключать более качественные адаптеры. Они начали с адаптеров для двух SIM-карт, а теперь перешли к адаптерам ради SIM-карт, которые позволяют вам совмещать четыре иначе даже пять SIM-карт в вашем телефоне.
    Установка двух SIM-карт
    SIM-карты в большинстве телефонов GSM устанавливаются под аккумулятором. В зависимости от устройства SIM-карта может вставляться в слот, скользить почти клипсой тож помещаться в клетку. Держатель SIM-карты alias слоты обычно пронумерованы, а SIM-карта вашего обычного оператора вставляется в слот 1. Некоторые модели имеют дополнительный слот ради SIM-карты снаружи. Ежели вы не видите часть порта, обратитесь к руководству по телефону, дабы узнать, который порт используется сообразно умолчанию.
    Активация карты
    Сотовые телефоны не подключены к тенета однако период ожидания звонка. Антенна потребляет большую клочок заряда аккумулятора телефона, следовательно большинство телефонов проверяют сеть исключительно каждые скольконибудь секунд. Вот почему время работы телефона в режиме ожидания намного больше, чем сезон разговора. Для некоторых телефонах с двумя SIM-картами телефон проверяет наличие вызовов для одной карте, а после проверяет другую. Разве телефон не поддерживает эту функцию, надо вручную переключить SIM-карту. Проверьте меню «Настройки» телефона на наличие меню «Настройки вызова» или «Параметры вызова».
    Недостатки двух SIM-карт
    Поскольку мобильный телефон имеет всего одну антенну чтобы совершения и приема вызовов, разом может фигурировать активна единственно одна SIM-карта. Примем, вы не можете гласить по телефону на одной SIM-карте и пить вызов на новый SIM-карте. Любые входящие вызовы, полученные для другую SIM-карту во время разговора по телефону, будут направляться прямо на голосовую почту, даже на телефонах, которые могут испытывать обе SIM-карты на наличие входящих вызовов. Эра автономной работы на телефонах, которые проверяют моментально обе симки, короче, потому сколько чаще активна антенна.

  62. Телефоны с двумя SIM-картами, якобы они работают?
    Onecom, крупнейший независимый бутафор телекоммуникационных услуг в Великобритании 23 августа 2019 г. Онеком ,Блог , мобильный
    У вас есть проблема с тем, чтобы таскать с собой рабочий и субъективный телефоны одновременно? Это может надевать неуклюжим и часто сбивает с толку нужда переключения между ними. Всетаки лопать решение — телефоны с двумя SIM-картами . Смотри тут самый дешевый сенсорный телефон за 1000 https://smartfonresurs.ru/xiaomi-redmi-note-8-64-gb-dve-sim-karty-xiaomi/ телефоны очень дешевые сенсорные.
    И поскольку весь новые устройства Samsung сегодня поставляются с опциями Dual SIM, мы подумали, сколько проведем вас чрез нужда узнать информацию, дабы вы могли решить, может ли она водиться вам полезна…
    Одна трубка
    Идеально подходит ради тех, у кого жрать ровно работник, беспричинно и индивидуальный телефон. Вы можете иметь два телефонных номера разом! Это означает, который вам не нужно надевать с собой два телефона иначе менять SIM-карты. Телефоны с двумя SIM-картами умны и дадут вам бомонд, сообразно который линии поступает требование или текст, следовательно вы сможете различать, является ли это деловым alias личным вызовом, вовремя чем ответить.
    Вы не привязаны к тенета
    Телефоны с двумя SIM-картами не привязаны к конкретной козни, что означает, сколько вы можете зарегистрироваться у любого провайдера, что вам нравится. Это помогает в международных поездках, не беспокоясь о разблокировке телефона разве покупке нового. Иначе вы можете воспользоваться хорошими тарифными планами чтобы голосовой связи одного поставщика и тарифными планами чтобы передачи данных другого поставщика, который даст вам лучшее из обоих миров!
    Какие существуют режимы работы с двумя SIM-картами?
    Существует 3 различных типа, наиболее популярным из которых является DSDS…
    Пассивный порядок с двумя SIM-картами (DSS):
    В пассивном телефоне с двумя SIM-картами дозволено использовать две разные SIM-карты, однако только одна из них может заключаться активной в любой момент времени. Это означает, который если одна SIM-карта работает, другая недоступна. Воеже использовать вторую SIM-карту, вам нужно активировать ее вручную, и присутствие этом первая SIM-карта деактивируется.
    Две SIM-карты, двойной порядок ожидания (DSDS)
    Гибрид посреди Dual SIM Standby и Dual SIM Dual Active. Они оба активны, токмо ежели вы их не используете. Коль обе SIM-карты находятся в режиме ожидания, вы можете исполнять и брать вызовы на любой из них. Всетаки, наравне лишь вы принимаете требование для одной SIM-карте, другая становится неактивной перед тех пор, пока первая карта не перестанет использоваться.
    Две SIM-карты, две активные (DSFA)
    Эта реализация позволяет совершать телефонные звонки с обеих SIM-карт внутри вашего смартфона. Он также может брать звонки на любую из двух SIM-карт одновременно. Обе SIM-карты ежеминутно активны.
    Хотите узнать больше?
    Разве вы заинтересованы в книга, для как узнать, как две SIM-карты могут приходить пользу вашему бизнесу, свяжитесь с нами, воеже обсудить это с членом нашей команды экспертов, что будет радовать ответить для любые ваши вопросы и предложить вам индивидуальное решение, позвоните нам.

  63. Как вы можете обладать четыре или пять SIM-карт в своем iPhone иначе Android-смартфоне
    Хоть сегодня некоторый высококлассные смартфоны поддерживают более одной SIM-карты, иногда вам нуждаться больше. Намного больше.
    Для людей, которые хотят разделить свою работу и домашнюю живот либо облако путешествуют по разным странам, возможность переключения промеж SIM-картами в вашем смартфоне имеет бесчисленный смысл. И хоть большинство смартфонов высокого класса сейчас поддерживают изрядно SIM-карт, вам может понадобиться больше. Сиречь, возможно, вы используете ветхий смартфон, в котором упихивать только единственный слот чтобы SIM-карты. Смотри тут дешевые телефоны сенсорные https://smartfonresurs.ru/xiaomi-mi-10-5g-128-gb-odna-sim-karta-xiaomi/ дешевые телефоны сенсорные связной.
    Вытаскивание лотка ради SIM-карты и забава с жестяными SIM-картами — это приказ потери SIM-карты иначе, что опять хуже, лотка. Утеря лотка ради SIM-карты — это настоящая головная печаль, скажу я вам!
    Избавьте себя через хлопот и приобретите снаряд, позволяющий использовать порядком SIM-карт.
    SIMore уже много лет производит адаптеры ради SIM-карт, и они продолжают исключать более качественные адаптеры. Они начали с адаптеров для двух SIM-карт, а теперь перешли к адаптерам для SIM-карт, которые позволяют вам совмещать четыре тож даже пять SIM-карт в вашем телефоне.
    Установка двух SIM-карт
    SIM-карты в большинстве телефонов GSM устанавливаются почти аккумулятором. В зависимости через устройства SIM-карта может вставляться в слот, скользить около клипсой или утверждаться в клетку. Держатель SIM-карты или слоты обычно пронумерованы, а SIM-карта вашего обычного оператора вставляется в слот 1. Некоторые модели имеют дополнительный слот для SIM-карты снаружи. Когда вы не видите часть порта, обратитесь к руководству сообразно телефону, для узнать, который порт используется по умолчанию.
    Активация карты
    Сотовые телефоны не подключены к путы все пора ожидания звонка. Антенна потребляет большую черепок заряда аккумулятора телефона, следовательно большинство телефонов проверяют козни лишь каждые скольконибудь секунд. Вот почему пора работы телефона в режиме ожидания намного больше, чем дата разговора. На некоторых телефонах с двумя SIM-картами телефон проверяет наличие вызовов для одной карте, а затем проверяет другую. Буде телефон не поддерживает эту функцию, нуждаться вручную переключить SIM-карту. Проверьте меню «Настройки» телефона на наличие меню «Настройки вызова» сиречь «Параметры вызова».
    Недостатки двух SIM-карт
    Поскольку мобильный телефон имеет всего одну антенну ради совершения и приема вызовов, сразу может фигурировать активна единственно одна SIM-карта. Положим, вы не можете излагать сообразно телефону на одной SIM-карте и принимать вызов на второй SIM-карте. Любые входящие вызовы, полученные для другую SIM-карту во время разговора по телефону, будут адресоваться сам на голосовую почту, даже для телефонах, которые могут испытывать обе SIM-карты для наличие входящих вызовов. Время автономной работы для телефонах, которые проверяют сразу обе симки, короче, потому сколько чаще активна антенна.

  64. Телефоны с двумя SIM-картами, подобно они работают?
    Onecom, крупнейший свободный бутафор телекоммуникационных услуг в Великобритании 23 августа 2019 г. Онеком ,Блог , мобильный
    У вас грызть проблема с тем, чтобы таскать с собой рабочий и субъективный телефоны одновременно? Это может содержаться неуклюжим и почасту сбивает с толку нужда переключения промеж ними. Впрочем лупить приговор — телефоны с двумя SIM-картами . Смотри тут дешевые телефоны сенсорные в оренбурге https://smartfonresurs.ru/xiaomi-redmi-note-8-64-gb-dve-sim-karty-xiaomi/ самый дешевый сенсорный телефон самсунг.
    И поскольку однако новые устройства Samsung сегодня поставляются с опциями Dual SIM, мы подумали, который проведем вас через нужда испытывать информацию, для вы могли решить, может ли она составлять вам полезна…
    Одна трубка
    Идеально подходит чтобы тех, у кого есть будто работник, беспричинно и личный телефон. Вы можете совмещать два телефонных номера одновременно! Это означает, который вам не нужно перемещать с собой два телефона иначе менять SIM-карты. Телефоны с двумя SIM-картами умны и дадут вам аристократия, по который линии поступает требование или текст, поэтому вы сможете узнавать, является ли это деловым либо личным вызовом, загодя чем ответить.
    Вы не привязаны к узы
    Телефоны с двумя SIM-картами не привязаны к конкретной сети, который означает, что вы можете зарегистрироваться у любого провайдера, что вам нравится. Это помогает в международных поездках, не беспокоясь о разблокировке телефона alias покупке нового. Или вы можете воспользоваться хорошими тарифными планами для голосовой связи одного поставщика и тарифными планами для передачи данных другого поставщика, который даст вам лучшее из обоих миров!
    Какие существуют режимы работы с двумя SIM-картами?
    Существует 3 различных типа, наиболее популярным из которых является DSDS…
    Пассивный порядок с двумя SIM-картами (DSS):
    В пассивном телефоне с двумя SIM-картами дозволено пользоваться две разные SIM-карты, но токмо одна из них может заключаться активной в любой момент времени. Это означает, что когда одна SIM-карта работает, другая недоступна. Дабы использовать вторую SIM-карту, вам надо активировать ее вручную, и около этом первая SIM-карта деактивируется.
    Две SIM-карты, двойной строй ожидания (DSDS)
    Гибрид среди Dual SIM Standby и Dual SIM Dual Active. Они пара активны, только коль вы их не используете. Коли обе SIM-карты находятся в режиме ожидания, вы можете делать и принимать вызовы для любой из них. Всетаки, ровно лишь вы принимаете вызов на одной SIM-карте, другая становится неактивной прежде тех пор, временно первая карта не перестанет использоваться.
    Две SIM-карты, две активные (DSFA)
    Эта действие позволяет совершать телефонные звонки с обеих SIM-карт внутри вашего смартфона. Он также может принимать звонки на любую из двух SIM-карт одновременно. Обе SIM-карты постоянно активны.
    Хотите узнать больше?
    Коли вы заинтересованы в том, чтобы действительно испытывать, наравне две SIM-карты могут приходить пользу вашему бизнесу, свяжитесь с нами, воеже обсудить это с членом нашей команды экспертов, какой довольно желать ответить для любые ваши вопросы и предложить вам индивидуальное приговор, позвоните нам.

  65. Точно работают телефоны с двумя SIM-картами?
    Что-то, сколько мы заметили около покупке телефонов с двумя SIM-картами, заключается в том, что деятель колоссально редко предоставляет какую-либо информацию о функциональности, кроме того, сколько она существует. В нем не говорится, ровно для практике работает функция двух SIM-карт, поддерживают ли обе SIM-карты 4G/5G и даже SIM-карты какого размера они принимают.
    Смотри тут самые дешевые телефоны сенсорные с интернетом https://smartfonresurs.ru/huawei-y7-2019-32-gb-dualsim-huawei/ сенсорные дешевые телефоны самсунг.
    Вы никогда не можете собираться; вам нуждаться довольно связаться с производителем или проверить таблицы спецификаций, обзоры иначе форумы, для испытывать эту информацию.
    Во всех телефонах с двумя SIM-картами, которые мы тестировали, обе SIM-карты постоянно находятся в режиме ожидания (так называемые телефоны с двумя SIM-картами), однако вы можете активно пользоваться всего одну SIM-карту после раз. Это означает, который любая SIM-карта может принять телефонный звонок alias текстовое известие в любое эпоха без необходимости активного переключения промеж ними сиречь перезагрузки телефона.
    Впрочем, ежели вы получаете требование для безраздельно номер, в то дата наподобие требование активен для другом, он не начнет звонить вам в ухо тож не даст вам мочь перевести первого звонящего на удержание – требование простой не будет успешным.
    В чем отличие среди Dual-Standby и Dual-Active?
    Телефоны с двумя активными SIM-картами используют два модема и позволяют принимать звонки враз на пара номера.
    Ежели вы хотите позвонить alias отправить текст, в Android наедаться стандартное меню «Господство SIM-картой», которое позволяет вам указать, какая SIM-карта должна использоваться ради голосовых вызовов, видеовызовов, сообщений и мобильных данных. Вы можете либо указать конкретную SIM-карту ради каждой из этих задач, либо оставить параметр «Навеки допрашивать».
    Если мастерство доходит предварительно телефонов с двумя SIM-картами, подключение ради передачи данных вызывает видимоневидимо путаницы. В то эра только оба слота чтобы SIM-карт на некоторых телефонах с двумя SIM-картами могут помогать соединения 4G или 5G, вы можете одновременно пользоваться подключение ради передачи данных лишь для одной SIM-карте.
    В предпочтение через звонков и текстовых сообщений, обычно соединение для передачи данных не может скрываться в режиме ожидания ради обеих SIM-карт; вы должны указать, какую SIM-карту вы хотите извлекать, а не отбирать ее около появлении запроса — что некоторые телефоны позволяют вам настроить их на переключение на другую SIM-карту, когда первая не может установить соединение.
    По умолчанию, когда вы используете подключение для передачи данных на одной SIM-карте, а телефонный звонок поступает для другую, он приостанавливает подключение для передачи данных для первой.
    Выбор смартфона или планшета — это один начало. В этом мире постоянного подключения качество и проворство выбранной вами тенета имеют решающее разум для вашей способности сидеть и шалить в дороге. Но какая мобильная козни лучше? Что простого ответа не существует, мы здесь, для помочь вам решить, какая сеть лучше только соответствует вашим потребностям.
    Возможность подключения может варьироваться через региона к региону и изо дня в день. Посетите веб-сайты всех основных игроков, и они скажут вам, сколько всюду у них отличное покрытие. Хотя больше нюансов.

  66. Подобно работают телефоны с двумя SIM-картами?
    Что-то, что мы заметили при покупке телефонов с двумя SIM-картами, заключается в книга, сколько виновник колоссально редко предоставляет какую-либо информацию о функциональности, кроме того, который она существует. В нем не говорится, ровно для практике работает занятие двух SIM-карт, поддерживают ли обе SIM-карты 4G/5G и даже SIM-карты какого размера они принимают.
    Смотри тут дешевые телефоны сенсорные до 2000 https://smartfonresurs.ru/huawei-y7-2019-32-gb-dualsim-huawei/ алиэкспресс телефон сенсорный дешевый.
    Вы никогда не можете собираться; вам надо будет связаться с производителем alias проверить таблицы спецификаций, обзоры иначе форумы, воеже узнать эту информацию.
    Во всех телефонах с двумя SIM-картами, которые мы тестировали, обе SIM-карты всегда находятся в режиме ожидания (так называемые телефоны с двумя SIM-картами), только вы можете активно извлекать как одну SIM-карту за раз. Это означает, сколько любая SIM-карта может принять телефонный звонок либо текстовое весть в любое время без необходимости активного переключения промеж ними alias перезагрузки телефона.
    Впрочем, если вы получаете вызов на одинокий комната, в то время якобы вызов активен на другом, он не начнет звонить вам в ухо тож не даст вам возможность перевести первого звонящего для удержание – вызов просто не будет успешным.
    В чем различие между Dual-Standby и Dual-Active?
    Телефоны с двумя активными SIM-картами используют два модема и позволяют пить звонки враз на пара номера.
    Если вы хотите звать или отправить текст, в Android потреблять стандартное список «Господство SIM-картой», которое позволяет вам указать, какая SIM-карта должна использоваться чтобы голосовых вызовов, видеовызовов, сообщений и мобильных данных. Вы можете либо указать конкретную SIM-карту чтобы каждой из этих задач, либо оставить параметр «Вечно спрашивать».
    Если дело доходит накануне телефонов с двумя SIM-картами, подключение ради передачи данных вызывает видимоневидимо путаницы. В то время как оба слота для SIM-карт для некоторых телефонах с двумя SIM-картами могут поддерживать соединения 4G разве 5G, вы можете одновременно пользоваться подключение ради передачи данных только для одной SIM-карте.
    В отличие от звонков и текстовых сообщений, обычно сливание ради передачи данных не может быть в режиме ожидания чтобы обеих SIM-карт; вы должны указать, какую SIM-карту вы хотите использовать, а не отбирать ее быть появлении запроса — чтобы некоторые телефоны позволяют вам настроить их на переключение на другую SIM-карту, если первая не может установить соединение.
    Сообразно умолчанию, если вы используете подключение ради передачи данных для одной SIM-карте, а телефонный звонок поступает для другую, он приостанавливает подключение чтобы передачи данных на первой.
    Отбор смартфона alias планшета — это единственно начало. В этом мире постоянного подключения покрой и живость выбранной вами сети имеют решающее разум чтобы вашей способности корпеть и шалить в дороге. Только какая мобильная сеть лучше? Хотя простого ответа не существует, мы здесь, воеже помочь вам решить, какая козни лучше только соответствует вашим потребностям.
    Мочь подключения может варьироваться через региона к региону и изо дня в день. Посетите веб-сайты всех основных игроков, и они скажут вам, который везде у них отличное покрытие. Правда больше нюансов.

  67. Телефоны с двумя SIM-картами, подобно они работают?
    Onecom, крупнейший самостоятельный бутафор телекоммуникационных услуг в Великобритании 23 августа 2019 г. Онеком ,Блог , мобильный
    У вас есть задача с тем, чтобы носить с собой рабочий и субъективный телефоны одновременно? Это может существовать неуклюжим и зачастую сбивает с толку необходимость переключения промеж ними. Всетаки лупить приговор — телефоны с двумя SIM-картами . Смотри тут самые дешевые но хорошие телефоны сенсорные https://smartfonresurs.ru/xiaomi-redmi-note-8-64-gb-dve-sim-karty-xiaomi/ телефоны с сенсорным экраном дешева.
    И поскольку однако новые устройства Samsung теперь поставляются с опциями Dual SIM, мы подумали, что проведем вас через необходимость испытывать информацию, чтобы вы могли решить, может ли она составлять вам полезна…
    Одна трубка
    Идеально подходит для тех, у кого есть будто рабочий, беспричинно и собственный телефон. Вы можете владеть два телефонных номера разом! Это означает, сколько вам не нуждаться перемещать с собой два телефона разве менять SIM-карты. Телефоны с двумя SIM-картами умны и дадут вам аристократия, по который линии поступает требование или текст, поэтому вы сможете отличать, является ли это деловым alias личным вызовом, вовремя чем ответить.
    Вы не привязаны к узы
    Телефоны с двумя SIM-картами не привязаны к конкретной путы, сколько означает, который вы можете зарегистрироваться у любого провайдера, кто вам нравится. Это помогает в международных поездках, не беспокоясь о разблокировке телефона или покупке нового. Иначе вы можете воспользоваться хорошими тарифными планами для голосовой связи одного поставщика и тарифными планами для передачи данных другого поставщика, что даст вам лучшее из обоих миров!
    Какие существуют режимы работы с двумя SIM-картами?
    Существует 3 различных типа, наиболее популярным из которых является DSDS…
    Пассивный строй с двумя SIM-картами (DSS):
    В пассивном телефоне с двумя SIM-картами дозволено использовать две разные SIM-карты, но один одна из них может красоваться активной в всякий момент времени. Это означает, сколько если одна SIM-карта работает, другая недоступна. Дабы использовать вторую SIM-карту, вам надо активировать ее вручную, и присутствие этом первая SIM-карта деактивируется.
    Две SIM-карты, двойной строй ожидания (DSDS)
    Гибрид промеж Dual SIM Standby и Dual SIM Dual Active. Они пара активны, токмо буде вы их не используете. Когда обе SIM-карты находятся в режиме ожидания, вы можете совершать и принимать вызовы для любой из них. Всетаки, наравне один вы принимаете требование на одной SIM-карте, другая становится неактивной до тех пор, покамест первая карта не перестанет использоваться.
    Две SIM-карты, две активные (DSFA)
    Эта реализация позволяет делать телефонные звонки с обеих SIM-карт внутри вашего смартфона. Он также может пить звонки на любую из двух SIM-карт одновременно. Обе SIM-карты неумолчно активны.
    Хотите испытывать больше?
    Разве вы заинтересованы в часть, воеже точно узнать, сиречь две SIM-карты могут принести пользу вашему бизнесу, свяжитесь с нами, для обсудить это с членом нашей команды экспертов, который довольно довольный ответить для любые ваши вопросы и предложить вам индивидуальное решение, позвоните нам.

  75. Программа сайт: kinostudiyawindowslive.ru для организации равным образом редактирования ютуб, втискивающаяся в течение состав пакета «Узловые элементы Windows». Ранние версии Windows Talkie Maker распространялись в течение составе Windows Me, Windows XP также Windows Vista, один-другой выходом Windows 7 Киностудия иметься в наличии выставлена с операционной строи Windows.

  79. Android Inc. была основана в течение Пало-Альто, штат Астероид, на октябре 2003 лета Энди Рубином, Ричем Майнером, Ником Сирсом а также Крисом Уайтом. Рубин обрисовал фотопроект Android яко обладающий «очень большим потенциалом в исследованию более умных подвижных приспособлений, каковые унше осведомлены что касается местонахождении а также предпочтениях свойского обладателя». Первоначальные планы братии состояли в течение исследованию передовой операционной системы чтобы числовых камер, а также это находилось фундаментом ее предложения инвесторам на апреле 2004 года. https://smartfonresurs.ru/optimizaciya-windows-10-kak-uskorit-pk-i-noutbuk-razgonyaem-i-uvelichivaem-proizvoditelnost-operacionnoj-sistemy/ Затем компания решила, яко рынок видеокамер ущербно двухколесник для актив нее круглее, а также число чуть-чуть месяцев через она отвлекла собственные действия да представила Android яко операционную систему чтобы мобильных телефонов, коя имела возможность бы составлять конкуренцию один-другой Симбиан равным образом Microsoft Windows Mobile.
    ЯЗЫК Rubin предстать перед взором препятствия немного привлечением инвесторов на ранешном этапе, а Android столкнулись кот выселением с офиса. Стив Перлман, близкий друг Рубина, произвести на свет ему 10 000 $ наличными в конверте и еще через малое время через некоторое время этого перевел неразоблаченную необходимую сумму в течение качестве начального финансирования. Перлман отперся через доли в течение компании также высказал: «Я сделал это, так как что доверял в течение этто и предполагал помочь Энди».
    В 2005 годку Рубин пытался стакнуться о сделках со Samsung равно HTC. Вскоре после сего в июле того же года Google приобрела компанию яко минимум за 50 млн. долларов; по обещаниям Дэвида Лоуи, старого вице-президента Гугл по корпоративному развитию, в течение 2010 г. этто была «лучшая шахер-махер Google». Центральные сотрудники Android, в течение этом численности Яхонт красный, Майнер, Сирс а также Уайт, подстроились к Google в течение рамках приобретения. В ТЕЧЕНИЕ то ятси о скрытной Android Inc. существовало ясный путь малое, так как компания предоставила мало подробностей, кроме того, яко она создавала программное энергообеспечивание для мобильных телефонов. В ТЕЧЕНИЕ Гугл ювентус под наставлением Рубина разработала платформу чтобы мобильных определений сверху складе ядра Linux. Гугл продавал платформу изготовителям подвижных телефонных аппаратов да операторам узы, обещая выделить эластичную систему раз-два возможностью обновления. Гугл «построил ряд партнеров числом аппаратным составляющим а также программному обеспечению да дал постигнуть операторам связи, яко распахнут чтобы различных степеней совместной работы».
    Слухи что касается плане Google кончаться сверху ярмарка подвижной связи возобновляли брать силу ут декабря 2006 года. Ранний спортпрототип был очень похож на эбонитовый друг BlackBerry, без сенсорного экрана (а) также раз-другой физической QWERTY-клавиатурой, но явление Apple iPhone в 2007 г. означало, яко Android «был вернуться к чертежной доске». Позже Google обманул свои доказательства спецификации Android, объявив, что «воспринимающие экраны довольно поддерживаться», хотя бы «Продукт был сконструирован начиная с. ant. до учетом наличия дискретных физических клавиш на свойстве предположения, поэтому чувствующий экран не что ль чистяком сменить физиологические кнопки». КО 2008 годку и Nokia, равно BlackBerry рекламировали телефоны кот сенсорным экраном, чтобы соперничать вместе с iPhone 3G, и в течение последнем финале фокус Android переключился на сенсорные экраны. Первоначальным с точки зрения прибыли недорогим смартфоном под правлением Android следовательно HTC Illusion, также известный как T-Mobile G1, анонсированный 23 сентября 2008 года.

  80. Официальный промокод 1хбет при регистрации только один, только по нему ты получишь бонус в 32 000 рублей, все остальные коды не действительные и не дают такой бонус. промокод 1 икс бет

    промо код для 1xbet

  81. Официальный промокод 1хбет при регистрации только один, только по нему ты получишь бонус в 32 000 рублей, все остальные коды не действительные и не дают такой бонус. промо для 1xbet

    промо 1xbet

  87. Tumour necrosis factor antagonists structure, function, and tuberculosis risks cialis 20mg In the prospective bone subprotocol of the ATAC trial n 308, 2 years of anastrozole significantly reduced LS BMD by 3

  104. Мосоптторг – зарекомендованная, востребованная, результативная компания, осуществляющая высококачественное обслуживание http://snabzhenie-obektov.ru/ для обеспечения материалами, применяемыми в строительстве.

  107. На сайте https://megapolis-plit.ru/ ознакомьтесь с огромным выбором тротуарной плитки и брусчатки от производителя, а также с услугами по профессиональной укладке тротуарной плитки в Краснодаре. Гарантия качества на продукцию и услуги, доступная цена от производителя, бесплатная смета, консультация и квалифицированное выполнение услуг любой сложности.

  108. На сайте https://apps.apple.com/us/app/va-vada-royal-castle/id6463615585 вы сможете сыграть в интересную игру и даже получить за это много бонусов, а при успешном выполнении задания перейти на новый уровень. Каждого игрока ожидают интересные битвы – они помогут проверить вашу мудрость, а также то, как вы владеете оружием. В этой игре предусмотрено огромное количество врагов, с которыми вам предстоит сразиться. В конце страницы представлена вся необходимая информация об игре и ее технические характеристики.

  109. Стоматологическая клиника https://kovalskii.dental/ в Хабаровске это лучшая новая стоматология, которая предлагает большой выбор услуг по приятным ценам. Мы оказываем услуги: лечение и профилактика, имплантация зубов, протезирование зубов, исправление прикуса, детская стоматология. Комфортная и доступная стоматология к вашим услугам с квалифицированными специалистами в своей области.

  110. On the website https://justfilm.org/ you can track the release dates of your favorite TV shows and get complete information about them. A large selection of trailers, TV shows from top and popular directors and various channels will give you the opportunity to study in advance what interests you, as well as add to the list for future viewing.

  111. На сайте https://play.google.com/store/apps/details?id=com.balljump.rememberwhat вы сможете поиграть в увлекательные и интересные игры, представленные лучшими разработчиками. Так вы получите огромный опыт в данной сфере и станете профессионалом. Перед вами огромный выбор слотов, а также интересных настольных игр, живых дилеров. В такие игры вы сможете сыграть на настоящие деньги и сорвать неплохой куш. Многие пользователи играют просто ради удовольствия и для того, чтобы разнообразить досуг.

  114. На сайте https://xn—-7sbbppfjc7awwmj.xn--p1ai/ вы сможете заказать стильный, красивый фартук для кухни – скинали. Они выполнены в самых разных стилях. Можно подобрать вариант с абстракциями, текстурами, флористикой, природой, городами, восточной тематикой. Важным преимуществом фартуков является то, что они надежные, отлично спасают от брызг жира и придают помещению привлекательный и красивый внешний вид. У вас получится связаться со специалистами напрямую и задать все интересующие вопросы.

  115. На сайте https://play.google.com/store/apps/details?id=com.fooooo00tba11.tetris сыграйте в казино, которое предлагает огромное количество игр на самый взыскательный вкус. Вавада представляет собой один из самых популярных онлайн-казино, которое по достоинству оценено соотечественниками. Оно постоянно устраивает различные акции, радует щедрыми бонусами. Кроме того, применяется софт от лучших разработчиков, которые зарекомендовали себя с лучшей стороны. У казино имеется лицензия, которая подтверждает законность действий.

  116. Visit https://50centtickets.org/ to purchase prime seat tickets and VIP packages for 50 Cent’s upcoming concerts in 2023/2024. Check out the schedule of events, find a suitable and convenient concert and be sure to attend the event.

  117. На сайте https://rezumepro.com/ воспользуйтесь такой важной и нужной услугой, как составление профессионального резюме. Сервис располагает первоклассными специалистами, у которых огромный опыт. В обязательном порядке практикуется индивидуальный подход. По этой причине резюме составляется с учетом особенностей отрасли. Вы сможете работать напрямую со специалистом, который в обязательном порядке возьмет на вооружение ваши пожелания. Высококлассные специалисты сэкономят ваше время на том, чтобы создать работающее резюме.

  118. Томоград – сеть современных диагностических центров, всегда на страже Вашего здоровья! Компания специализируется на современных методах диагностики, включая МРТ, КТ УЗИ и рентген. Центры располагаются на территории Кубани, что делает доступ к качественной диагностике максимально удобным. Современное оборудование и опытные врачи обеспечивают точные и быстрые результаты, помогая вам заботиться о здоровье. Посетите сайт компании https://tomograd-kuban.ru/ чтобы получить подробную информацию и записаться на прием.

  119. На сайте https://nova-51.ru/detskaya-stomatologiya-murmansk/ вы сможете узнать все о детской стоматологии в Мурманске, где мы вылечим молочные зубы, научим соблюдать гигиену полости рта, исправим прикус у детей. Все процедуры проходят в комфортной обстановке, врач друг для ребенка, к которому он будет с удовольствием приходить на прием. Обращайтесь! Полная информация на сайте.

  121. On the website https://grandcanyontours.vegas/ you can book the best excursions around the GRAND CANYON from las vegas. Unique offers daily by luxury bus, helicopter, plane, boat. Discount Grand Canyon Tours from Las Vegas. Book your tour now for the best offer.

  122. На сайте https://eto-kino.com/ посмотрите фильмы, сериалы в идеальном качестве и прямо сейчас. Все они на самую разную тему и отличаются незаурядным сюжетом. Есть как драмы, так и мелодрамы, комедии, вестерны, исторические фильмы, триллеры, где играют любимые актеры. Все фильмы представлены в отличном качестве, с хорошим звуком, поэтому доставят только радость во время просмотра. Для того чтобы подобрать оптимальный вариант на вечер либо выходной день, необходимо воспользоваться специальным фильтром.

  123. На сайте https://export-plus.ru/ вы сможете ознакомиться с полной информацией и заказать экспортные поставки, импортные поставки, экспорт из России, импорт из России, таможенное декларирование, ВЭД. Широкий спектр услуг по комплексной организации импортных и экспортных поставок как для российских предприятий, так и для иностранных компаний. Мы работаем более 10 лет и оказываем только качественные услуги.

  124. На сайте https://www.pro-monument.ru узнайте телефон компании для того, чтобы заказать такую популярную и важную услугу, как изготовление, монтаж памятников, а также надгробий. Конструкции производятся из мрамора, гранита. Из-за того, что в компании трудятся высококлассные, опытные сотрудники, то они выполнят проект независимо от его сложности. Вы сможете заказать как элитные, так и эксклюзивные варианты. В стоимость включен весь спектр работ, в том числе, заливка бетона, облицовка, установка оград, столов.

  126. На сайте Центра ментального здоровья и психологического развития Эмпатия вы сможете узнать симптомы депрессии, депрессия получить консультацию и квалифицированное лечение.

  127. На сайте https://slc-company.ru/ вы сможете узнать все подробности для того, чтобы воспользоваться такой полезной услугой, как кадровое, бухгалтерское обслуживание. Кроме того, доступно юридическое сопровождение, которое организуется высококлассными, компетентными специалистами. Они учитывают все нюансы работы. Первый месяц бухгалтерского обслуживания бизнеса предоставляется абсолютно бесплатно. Вы сможете заказать полный спектр бухгалтерского сопровождения. Компания работает на рынке 14 лет, а потому выполнит все так, как нужно.

  128. On the website https://kenyabonus.com/ you can receive welcome bonuses and promotional codes for bets. A site with reviews of casinos and gaming platforms for betting on sports events with the best promotional codes for 2023!

  129. На сайте http://www.ideas4rent.ru вы сможете взять в аренду различную мебель, а также оборудование для любых мероприятий, включая детские праздники, конференции, фестивали. Оперативная доставка выбранного товара в любую точку России. Вся мебель произведена из качественных, надежных материалов, за счет которых она прослужит долгое время. Все изделия чистые, ухоженного внешнего вида, поэтому подойдут для мероприятия различного масштаба. Ознакомьтесь с кейсами компании прямо сейчас.

  131. На сайте https://easypayments.online/ вы сможете ознакомиться как зарегистрировать компанию за границей удаленно для приема международных платежей. Получите собственные аккаунты в платежных системах Stripe, Paypal и легально принимайте платежи со всего мира. Мы предлагаем лучшие решения для бесперебойного и стабильного приема платежей. Все преимущества на нашем сайте.

  132. На сайте https://www.amberrussia.ru/ вы сможете приобрести различные янтарные украшения, включая бусы, браслеты, а также иконы. Здесь также имеется и косметика, крестики, кулоны из янтаря, интересные сувениры, которые будет приятно получить всем. Богатый ассортимент позволит обязательно выбрать именно то, что нужно и для любого повода. Имеются изделия из янтаря для детей. Вся продукция реализуется по привлекательной стоимости, доступна оперативная доставка. Товары сертифицированные, отличаются высоким качеством и привлекательным видом.

  135. Жирные кислоты соапстоков светлых растительных масел и саломасов для кормовых віктор пономарчук vioil основными направлениями экспорта ViOil являются страны СНГ, Ближнего Востока.

  136. Сайт https://www.forklift.blog/ это лучший источник информации и профессиональное издание о подъемно-погрузочной технике. Только свежие, актуальные, экспертные статьи обзоры и новости о погрузочной и подъемной технике, с постоянным обновлением и пополнением. Можно прочитать как свежие статьи, так и горячие темы, что обязательно будет интересно специалистам в данной тематике.

  137. На сайте МУЗ ТВ https://muztv.org/ вы сможете скачать бесплатную музыку или слушать онлайн на сайте. Все новинки музыки, популярные песни, альбомы доступны в высоком качестве и без регистрации. Воспользуйтесь поиском по музыкальным трекам и найдите любимую музыку и песни для скачивания или подберите музыку под настроение из готовых вариантов треков.

  138. На сайте https://play.google.com/store/apps/details?id=com.light290.up623 вы сможете прокачать свой мозг, играя в удивительную, интересную головоломку, которая необходима для того, чтобы повысить логическое мышление. В этой игре необходимо соединить линии с той целью, чтобы получилось зажечь лампочки. Игра начинается с обычных упражнений, которые очень простые. С каждым турниром игра усложняется, вводятся новые элементы, а также бонусы. Данные пользователей не передаются третьим лицам, вся информация является конфиденциальной.

  143. На сайте https://m-strop.by/ закажите стропы текстильные, грузовые, канатные, а также различные грузозахватные приспособления. Важным преимуществом компании является то, что она сама производит всю продукцию в соответствии с ГОСТом, самыми высокими нормативами, что позволяет предложить клиенту изделия высокого качества и в необходимом количестве. Вся продукция и в полном объеме хранится на складе. Доступна оперативная доставка во все регионы. Для всех оптовых покупателей действуют скидки. Совершайте выгодные покупки.

  144. Сайт https://xakertop.net/topic/110/page-6 представляет собой форум программистов и хакеров. Здесь вы сможете подобрать специалиста для того, чтобы взломать почту, получить пароли от почты или ВК. Кроме того, есть сотрудники, которые для вас взломают Вайбер, Вацап. Каждый заказ выполняется максимально быстро, чтобы вы получили мгновенный результат. Просто свяжитесь со специалистом удобным для вас способом. Все работы выполняются анонимно, конфиденциально, а о вашем обращении никто не узнает.

  148. Как начать играть в онлайн казино, секреты, советы, рейтинг Вавада Казино Как не проиграть все? Как выиграть? Брать бонус на депозит?

  149. На сайте http://klubmama.ru/ вы сможете ознакомиться с большой каталогом и фото поделок. Выберите из рубрик: новогодние поделки, поделки для малышей, осенние поделки, поделки своими руками, поделки из бутылок, поделки в школу, поделки маме, поделки для начинающих и десятков других рубрик, посмотрите фото и сделайте своими руками уникальные поделки и аппликации.

  151. На сайте https://avtolider40.ru/ оставьте заявку для того, чтобы записаться на занятия в автошколу. К ее важным преимуществам относят то, что здесь фиксированная стоимость, отсутствуют скрытые платежи. Есть возможность оплатить обучение в несколько этапов. Все инструкторы являются высококлассными специалистами, у которых огромный опыт работы. Они научат вас всему, а потому вы будете отлично водить автомобиль. График обучения составляется с учетом предпочтений, наличия свободного времени. Практикуется полное сопровождение.

  152. На сайте https://businessua.com.ua/ представлены новости на тему бизнеса, экономики, культуры, недвижимости, рынка, криптовалюты. Все материалы свежие, актуальные, поэтому ознакомиться с ними необходимо всем. Также представлены статьи на тему бизнеса, криптовалюты. Здесь имеется все, что вам так интересно. И самое главное, что все новости, статьи составлены лучшими специалистами, которые находят материалы в открытых источниках. Заходите сюда регулярно, чтобы почерпнуть что-то для себя и рассказать друзьям.

  153. На сайте https://uavisti.com/ ознакомьтесь с актуальными, свежими новостями Украины. Они касаются политики, экономики, а также спецоперации. Все данные являются достоверными, честными, поэтому ориентируйтесь на них. Имеются не только полезные статьи, но и видеоматериалы, которые прольют свет на многие вопросы. Опубликованы сведения о культуре, спорте. Все это позволит понять то, что происходит на Украине в данный момент. Имеются обзоры и все то, что позволит сделать выводы о происходящем.

  154. На сайте https://vun.com.ua/ изучите самые актуальные, свежие новости, которые будут интересны всем украинцам, без исключения. Имеются сведения про здоровье, о том, кто победит в боях, о том, когда выйдет трейлер к фильму. Много статей написано по теме политики. Есть мнения первых лиц государств, президента на счет ситуации на Украине. Обязательно посмотрите то, какая сегодня погода, а также ознакомьтесь с курсом валют. Регулярно на портале появляются свежие новости, с которыми необходимо ознакомиться всем.

  156. 1xBet – это благоприятные условия при регистрации и выборе ставок промокод 1xbet tj ринимая участие во всех выгодных предложениях, новички и постоянные игроки получают прекрасную возможность увеличить свой бонусный счёт.

  159. На сайте https://osvitanovyny.com/ ознакомьтесь с информацией, которая посвящена культуре, детям, а также семье. Очень много информации представлено на тему сохранения здоровья, о том, как выбрать профессию. Очень много контента на тему политики. Есть самые новые публикации на тему правильного питания, еды и того какая польза в зеленых овощах. Статьи созданы первоклассными авторами, которые отлично понимают в этих вопросах и предлагают вам расширить кругозор и повысить уровень знаний.

  160. На сайте https://polskiezycie.pl/ почитайте интересную, актуальную и свежую информацию на самые разные темы. Имеются материалы на тему политики, экономики, бизнеса, технологий, спорта и многого другого. Каждая хозяйка узнает о том, как приготовить вкусное и полезное блюдо на обед для всей семьи. Также есть прогноз погоды на ближайшую неделю. Имеются новости о популярных личностях. Есть данные на тему строительства, проведения ремонтных работ. Обязательно ознакомьтесь с информацией, посвященной технологиям.

  162. На сайте https://vehrrxcso.ru попытайте свою удачу и сыграйте в интересные, любопытные игры прямо сейчас. Перед вами огромный выбор слотов, включая Dice, Mines, Bubbles, Wheel, Plinko, которые пользуются огромной популярностью среди любителей азарта. Ежедневно на сайт заходит огромное количество пользователей, которые, как и вы, мечтают попытать свою удачу в этой игре. Этот сервис предоставляет уникальную возможность заработать свой процент на реферальной программе. Ежедневный бонус – это 100 рублей.

  163. На сайте https://1novyny.com/ ознакомьтесь с актуальными новостями на тему политики, бизнеса, экономики, культуры, спорта. Здесь опубликованы действующие и эффективные лайфхаки, которые помогут вам приобрести именно то, что необходимо, не тратя лишних денег на ненужные покупки. Имеются статьи на тему войны, высказывания президента Украины и мнения первых лиц на ситуацию вокруг России и Украины. Для того чтобы вы лучше освоили информацию и нашли ту новость, которая важна в данный момент, весь контент поделен на специальные разделы.

  164. На сайте https://worldbts.com/ получите всю необходимую, актуальную и свежую информацию на тему криптовалюты, биткоинов. Здесь вы сможете почитать материал о каждом виде криптовалюты, ее достоинствах и ознакомиться с другими важными моментами. Есть информация о криптовалюте в Грузии. Также имеются данные и о трейдинге. Опубликованы различные любопытные и интересные новости, которые важны для тех, кто интересуется этим направлением и желает побольше узнать об этой сфере. Регулярно публикуется новая информация, новости, которые помогут вам всегда быть в курсе всего происходящего.

  165. На сайте https://newsfin.pl/ ознакомьтесь со свежими, актуальными новостями на тему недвижимости, финансов. Перед вами самые последние новости не только Польши, но и всего мира. Они сопровождаются красочными тематическими картинками, которые помогут лучше разобраться в теме. Ежедневно на сайте появляются новые данные, с которыми необходимо ознакомиться и вам. Все статьи составлены талантливыми авторами, которые выбирают самую суть, чтобы вы получили исчерпывающий ответ на свой вопрос.

  166. На сайте https://zoovet36.ru/ узнайте телефон ветеринарной клиники «Зоовет 36», где смогут вылечить ваше домашнее животное в 2 счета. Здесь есть цифровой рентген, а также собственная лаборатория, отдел ортопедии, хирургии. Вашему животному будет оказан весь надлежащий уход. Важным моментом является то, что в клинике принимают только врачи высшей категории. Они используют инновационные и уникальные препараты, высокотехнологичное оборудование, которое быстро определит причину недуга.

  168. На сайте https://bashni.pro ознакомьтесь с самыми популярными новостройками, которые находятся в Приморском крае. Для того чтобы подобрать лучший вариант, необходимо обозначить город, а также улицу. Кроме того, следует выяснить, какой вариант вы предпочитаете – с отделкой либо без. Также обозначьте стоимость, на которую вы рассчитываете, и площадь. На сайте вы найдете и нужные новости, если вы интересуетесь данной темой. Также на портале представлены и видеоматериалы, которые ответят на многочисленные вопросы.

  169. На сайте https://xn--36-6kcao3cdj.xn--p1ai/ вы сможете приобрести мангалы, которые представлены здесь в огромном количестве. Также здесь находятся и грили, барбекю, шампуры, коптильни, решетки и многое другое. Кроме того, есть возможность заказать различные печи самого разного размера и под казан. Присутствуют и подарочные наборы. Для того чтобы иметь представление о том, как все работает и какого качества, необходимо посмотреть видео. Вся продукция выполнена из качественного, надежного и практичного материала, который не теряет своих технических свойств.

  174. На сайте https://bigpicture.ru/ ознакомьтесь с интересными и увлекательными картинками, за которыми скрывается интересный, познавательный контент. Перед вами топ лучших новостей, которые необходимо изучить и вам. Есть интересные и любопытные фотографии, которые решили опубликовать только сейчас, спустя некоторое время. Вы узнаете и о том, почему девушки Вавилона пользовались таким успехом. Имеется гимнастика для ума. Кроме того, есть информация о самых интересных завтраках из различных уголков мира.

  175. Сайт https://www.svartk.ru/ представляет собой уникальный портал, на котором продают сварочное оборудование, а также различные материалы. В разделе представлено электросварочное оборудование, а также газопламенная аппаратура, материалы, предназначенные для выполнения профессиональных сварочных работ. Вы сможете купить продукцию по доступным ценам и с оперативной доставкой. Все необходимое получится приобрести оптом. Продукция соответствует ГОСТу, она сертифицированная, а потому наделена длительным сроком эксплуатации.

  177. На сайте https://mybitcoin.xyz/ вы сможете получить знания на тему блокчейна, высоких технологий, о биткоине. Кроме того, вы узнаете много информации о криптовалюте, которая потребуется тем, кто только начинает познавать данную сферу. Перед вами список тем, доступных для изучения. Вы узнаете об основах криптографии, о введении в блокчейн. Обязательно необходимо изучить информацию на тему того, как работает транзакция. Изучите материалы на тему криптовалютных кошельков. Ознакомьтесь с данными о майнинге.

  179. На сайте https://business-style.net/ имеется вся необходимая, актуальная информация, касающаяся таких сфер, как: красота и здоровье, бизнес-стиль, мода, питание, культура. Опубликованы содержательные и информативные статьи на тему моды на примере таких селебрити, как Кейт Миддлтон, Сара Джессика Паркер, Диана Крюгер. Имеется информация о культуре, разных популярных личностях, мнение которых для многих очень важное. Они высказываются на определенную тему. Есть и интервью с ними. Регулярно публикуются новые данные.

  183. На сайте https://play.google.com/store/apps/details?id=com.light290.up623 сделайте свои ставки в БК «Леон», которую ежедневно посещают несколько тысяч игроков. Они желают сорвать куш и получить больше приятных эмоций от игры. Даже если вы всего лишь несколько минут побываете на главной странице, то сразу станет понятно, что компания очень лояльно относится к клиентам и заинтересована в долгосрочных отношениях. Она может предложить огромный выбор слотов, высокие коэффициенты, а также бонусы, турниры.

  185. На сайте https://interesnews.com/ изучите интересные новости, которые касаются любопытных историй, здоровья, культуры, науки, животных, космоса и пространства. Есть колонка, которая называется «Странные новости», где выкладывается все очень необычное, что происходит в мире. Выкладываются фотографии артефактов, видеоматериалы. Есть любопытные данные о софе, которая считается оптимальным выбором для тех, кто желает спать с комфортом. Есть интересная информация по поводу планеты Земля.

  186. На сайте https://aifua.com.ua/ имеются свежие и интересные новости, актуальные данные на тему бизнеса, войны, медицины, технологий, спорта, культуры. Как только на Украине что-то происходит, то сразу же отображается в новостях на этом сайте. Они написаны высококлассными специалистами, которые отлично понимают в этой теме и освещают все вопросы максимально правдиво и честно. Регулярно публикуются свежие данные, новости, которые будут интересны всем, независимо от социального положения, возраста.

  187. День рождения моей дочери был на носу, а у меня не было денег на подарок, который она так хотела. Мне нужно было 8 000 рублей. Я обратился к mikro-zaim-online.ru в поисках помощи.

    Благодаря простой и понятной системе, я быстро нашел подходящее МФО. Заявка была одобрена в течение нескольких минут, и деньги поступили на мою карту. Дочь была счастлива, получив желанный подарок.

  188. На сайте https://www.oriservice.ru/ ознакомьтесь с информацией, посвященной компании Орифлейм. Здесь вы узнаете о том, как бесплатно зарегистрироваться, что для этого необходимо сделать. При этом каждая женщина сможет не только заниматься своим любимым делом, но и заказывать товары с хорошей скидкой и по лучшей стоимости. Заказывайте товары не только себе, но и своим родственникам, знакомым, друзьям. Орифлейм дарит отличную возможность заработка и покупки косметики для себя и со скидкой.

  189. На сайте https://centrua.com.ua/ имеется информация, которая касается политики, экономики, культуры, спецоперации и других важных направлений. Это авторитетное издание, которое предлагает ознакомиться только с честной информацией, которая будет вам полезна для расширения кругозора. Здесь также представлены и аналитические статьи, которые ответят на многие вопросы. Имеется интервью селебрити, популярных личностей, которые желают высказаться по поводу определенных проблем и того, что происходит в мире.

  190. На сайте https://123film.pro/ вы сможете посмотреть фильмы, новинки сериалов, мультики. Также есть и популярные произведения, которые вам захочется пересматривать раз за разом. Имеются фильмы и сериалы разных жанров: комедии, ужасы, исторические, документальные. Вы сможете воспользоваться фильтром для того, чтобы отсортировать произведения по году и стране выпуска. Среди огромного выбора вы точно подберете вариант, исходя из своих предпочтений и вкуса. Все фильмы в безупречном качестве, с хорошим и четким звуком, а потому точно произведут впечатление.

  192. Наши преподаватели, среди которых есть и носители языка, всегда готовы помочь Вам приобрести необходимые знания, курсы английского языка цены чтобы в дальнейшем их можно было уверенно использовать в повседневной жизни.

  193. На сайте https://narcoalco.ru вы сможете получить консультацию относительно лечения, а также реабилитации зависимых. В клинике вам будет предложен полный спектр всех необходимых услуг, включая вывод из наркотической, алкогольной зависимости. В обязательном порядке оказывается психологическая поддержка во время социальной адаптации. Компания активно работает, в том числе, и с несовершеннолетними. По России представлено более 6 центров. Зависимые лечатся по революционной технологии.

  194. На сайте https://shefpovar.com.ua/ вы сможете ознакомиться со вкусными, интересными рецептами, которые можно приготовить как на каждый день, так и большие праздники. Перед вами самая большая коллекция рецептов, которые вы сможете приготовить в домашних условиях. Есть способы приготовления первых блюд: свекольника, рассольника, борщей, супов, а также вторых – из овощей, мяса, морепродуктов. Есть рецепты салатов, заливного, выпечки, десертов. Все это сможет приготовить каждая женщина, даже с минимальным набором знаний и продуктов.

  195. На сайте https://newscrypto.net/ изучите актуальные, свежие новости, которые посвящены криптовалюте, майнингу. Для того чтобы подобрать определенную тему, необходимо воспользоваться специальным навигатором по сайту. Имеются такие разделы, как: «Анализы», «Маркет», «Майнинг», «Новости», «Технологии», «Трейдинг». Весь контент сопровождается интересными и цветными картинками для наглядности. Над материалом работают лучшие авторы, которые знают, какую информацию вам предоставить. Регулярно появляются свежие данные.

  197. На сайте https://allua.biz/ представлены актуальные и свежие новости главных событий, экономики, политики, бизнеса, науки, технологии и многое другое. Также здесь освещаются последние новости об Украине. На сайте вы получите оперативную и достоверную информацию из всех областей жизни общества. Регулярно посещая данный ресурс, вы можете быть точно уверены, что не пропустите ни одно событие из страны и мира. Все рубрики сгруппированы, что значительно облегчает поиск необходимой информации.

  198. На сайте https://play.google.com/store/apps/details?id=com.wildhearts.challengegame&hl=ru&gl=ru вы сможете сделать ставки на спорт в популярной конторе «Фонбет», которая предлагает огромный выбор спортивных состязаний на любой вкус. Ежедневно предлагается огромное количество вариантов ставок на самые разные спортивные состязания. Вам доступны высокие коэффициенты, предлагаются бонусы для каждого игрока. У вас получится пополнить счет абсолютно безопасно, после чего вывести средства.

  199. На сайте http://smartporog.ru можно заказать автоматические пороги по приемлемой цене. Сертифицированное производство с гарантией качества позволяет компании быть лучшей из крупнейших поставщиков порогов на ранке по всей территории РФ. Пороги, приобретенные здесь, подходят на двери из разного материала. Доставка по России осуществляется бесплатно. На сайте есть возможность ознакомиться с каталогом, а также сделать заказ по телефону. Оптовым покупателям предоставляются специальные цены.

  202. На сайте https://koppst.kr.ua/ получите важную информацию на тему, касающуюся агроправа, агробизнеса, фермерского хозяйства. Так вы узнаете о том, что в этом году на Украине было собрано рекордное количество гречки, про долю зарубежной свинины на рынке. Все статьи поделены на рубрики, что позволит отсортировать ненужную информацию и узнать только то, что действительно интересует в данный момент. Имеется информация, касающаяся местной продукции. Вы узнаете, почему подорожала молочная продукция.

  203. На сайте https://fakty.org/ вы сможете ознакомиться с самыми последними данными на тему экономики, здоровья, культуры, науки. Также можете взять контакты редакции. Есть информация на тему того, что происходит сейчас на Украине. Имеются любопытные и информативные статьи на тему экономики, бизнеса, а также криминала. Публикуются мнения первых лиц, а также ключевых фигур, которые ответят вам на многочисленные вопросы. Их мнения очень важны, ведь они подскажут вам много интересного, актуального, о чем вы еще не знали.

  204. На сайте https://garant-plus.ru/ представлены объекты недвижимости, которые вы сможете приобрести прямо сейчас. Агентство недвижимости «Гарант Плюс» предлагает свои услуги по сдаче, приобретению, аренде недвижимости в Москве и по области. Кроме того, есть возможность заказать дополнительные услуги. К примеру: оформление в собственность, подведение газа, различных коммуникаций, сбор документов для того, чтобы согласовать строительство, получить разрешение на ввод зданий. Компания работает с 1988 года, чтобы чувствовали себя максимально комфортно.

  205. На сайте https://xakertop.net/topic/110/page-6 вы сможете воспользоваться высококлассными услугами профессиональных хакеров. Они смогут с легкостью взломать электронную почту, выполнить детализацию СМС. Специалисты работают в данной сфере длительное время, а потому справятся с задачей независимо от ее сложности. При этом вас обрадуют привлекательные расценки. Результат вы получите в минимальные сроки. Специалисты смогут взломать социальные сети, а также получить все необходимые пароли.

  206. На сайте https://teplyy-pol77.ru/ заполните заявку для того, чтобы рассчитать цену установки теплого пола. Он позволит вам создать в доме необходимую атмосферу. Всего за 24 часа вы сможете получить качественное, надежное покрытие, которое позволит себя чувствовать комфортно. Теплый пол даст возможность вам сэкономить на отоплении, во время монтажа не потребуется стяжка. Предоставляются гарантии 15 лет. Нет магнитного поля, а потому покрытие является полностью безопасным. В компании можно заказать проектирование, оборудование, монтаж.

  207. На сайте https://svitzaxoplen.kr.ua/ вы сможете почитать любопытные, интересные данные, которые касаются правильного питания, того, как поддержать здоровье в определенном возрасте. Диетологи определили доступный способ, который поможет скинуть вес без лишних мучений. В разделе находится огромное количество полезной, годной информации, которая прольет свет на многие вопросы. Статьи написаны медиками, первоклассными специалистами, которые готовы предоставить исчерпывающую информацию.

  208. На сайте https://xn--80aaelrmlfr9a.su/ получите ценную и актуальную информацию о пневматике, ее правильной покупке, профессиональном и качественном обслуживании, проведении ремонтных работ. Вы почерпнете для себя очень много полезной информации, которая будет необходима, если у вас есть пневматика. Также имеется контент о боеприпасах, ремонте и апгрейде. Для того чтобы подыскать подходящий материал, необходимо воспользоваться поиском. Есть раздел со свежими записями от лучших и квалифицированных авторов.

  209. На сайте https://shemi-otopleniya.ru/ почитайте информацию о гибкой подводке, которая произведена из нержавеющей стали. Она представлена на сайте самой разной модификации и диаметра, что позволит подобрать вариант, исходя из требований, особенностей производства. Также на сайте вы сможете ознакомиться со всей необходимой информацией по поводу гибкой подводки. Вся продукция создается из качественных материалов, выполнена по ГОСТу, она сертифицированная. Для того чтобы подобрать то, что необходимо, воспользуйтесь специальным фильтром.

  210. Аутизм – описание заболевания, классификации, симптомы у взрослых и детей, причины появления заболевания, лечение аутизма методы диагностики и способы лечение недуга.

  211. На сайте https://intimpitera.com вы сможете ознакомиться с удивительными красотками, которые жаждут общения со своим господином. Они невероятно привлекательные, сексуальные и раскрепощенные, а потому смогут привести в восторг любого мужчину. И самое главное, что дамы ухоженного и привлекательного вида. У них подтянутая, спортивная фигура, которая понравится даже эстету. У девушек мягкие, нежные руки, они станцуют стриптиз и обрадуют своими эротическими играми. Есть возможность снять даму на час или несколько.

  212. На сайте https://cryptoinfor.com/ изучите исчерпывающую информацию, которая касается криптовалюты. Есть качественные, свежие новости, которые помогут получить ответы на многие вопросы. Так вы узнаете о том, какая самая популярная криптовалюта и за какой из них будущее. Ежедневно на сайте появляется новая информация, с которой будет интересно ознакомиться и вам, если вы хотите узнать побольше о криптовалюте. Вся информация подается в простой и понятной форме, а потому вы ее точно усвоите.

  213. На сайте https://layfhaki.com/ вы сможете получить всю необходимую информацию на самые разные темы: здоровье и красота, лайфхаки, интересное, дом и дизайн, секс. Эти ценные рекомендации помогут вам выполнить сложные задачи в 2 счета, быстро и не прикладывая к этому много сил. Рекомендации составлены лучшими специалистами, которые предложат актуальные данные, ценные советы. Они будут нужны всем, кто ищет советы на каждый день. Так вы узнаете о пользе авокадо, продуктах, которые скажутся на вашей психике, рисовой воде для красоты.

  214. На сайте https://xn--e1afajie1bv.xn--p1ai/ ознакомьтесь с продукцией компании «ХИМТЕК», которая производит не окисленные полиэтиленовые воски при помощи каталитической деструкции полимеров. Компания считается единственной в России, которая работает таким методом. Вы также найдете огромное количество актуальных тематических новостей, которые обязательно вас заинтересуют. Если и вас заинтересовало предложение, то заполните форму ниже, чтобы связаться. Обязательно ознакомьтесь с нормативными документами.

  215. На сайте https://vipprokat42.ru/ вы сможете ознакомиться с любыми видами автотранспорта. Вашему вниманию предлагается огромный выбор моделей качественных авто по лояльным ценам. Вы можете взять машину с персональным водителем либо заказать машину на праздники. Для того чтобы выполнить сделку заказа, необходимо найти подходящее автомобильное средство и заполнить форму онлайн. Здесь есть возможность оплаты различными способами. Помимо прочего, постоянным клиентам предлагаются бонусы, подарки и скидки.

  216. На сайте https://aptekamos.ru/ вбейте название лекарства для того, чтобы заказать его в ближайшей аптеке. Здесь также вы ознакомитесь с ассортиментом, а также расценками. Имеются и телефоны, адреса аптек. Изучите список аптек, которые предлагают оперативную доставку. Имеются такие заведения, которые работают в круглосуточном режиме. Предоставляется актуальная и свежая информация. Если и вы ищите какое-либо лекарство, то обязательно найдете его на этом портале. Почитайте последние новости, которые будут для вас полезны.

  217. На сайте http://bt-futures.ru/ вы узнаете подробную информацию для трейдера, а также интересные данные о том, как трейдеру научится больше зарабатывать и не перегореть. Здесь есть очень много нужного и полезного материала о финансовой системе. Чтобы погрузиться в рынок, нужно пройти изучение и использовать эффективные стратегии, об этом подробнее вы узнаете на сайте, где нужно пройти в соответствующий раздел. Также на портале есть возможность пройти этапы, по которым можно увеличить свою рентабельность от трейдинга в 2 – 3 раза.

  218. На сайте https://stolycia.com.ua/ вы сможете получить всю нужную информацию об экономике, бизнесе, медицине, здоровье и многом другом. Имеются данные о культуре. Есть и новые статьи, с которыми необходимо ознакомиться всем, кто проживает на Украине и переживает за свою страну. Имеется информация, которая касается транспорта и инфраструктуры. Вы ознакомитесь со всеми свежими данными, которые публикуются квалифицированными специалистами. Регулярно на сайте выкладываются новые статьи, которые прольют свет на многочисленные вопросы.

  219. На сайте http://smotrikinohd.ru вы найдете интересное и качественное кино. Здесь есть больше 30 тыс. фильмов и сериалов онлайн разных жанров, времен и народов. Команда проекта регулярно следит за обновлением фильмов и постоянно добавляет картины, чтобы пользователи могли наслаждаться лучшими мировыми шедеврами. На сайте есть удобный поиск, с помощью которого можно быстро отыскать необходимый фильм. Здесь каждый найдет что-то интересное для себя, а главное это то, что можно смотреть фильмы без регистрации и отправки смс!

  220. На сайте http://elekspb.ru вы сможете приобрести судовой кабель, судовую электротехнику с регистром и многое другое. «ЭЛЕК» считается наиболее популярным предприятием, которое не перестает развиваться. Оно активно поставляет материалы, а также электрооборудование. Вся продукция создана по ГОСТу, является сертифицированной, качественной, а потому никогда не подведет. Для того чтобы проконсультироваться, необходимо позвонить по обозначенному телефону. Таким же образом сделайте заказ.

  222. На сайте https://www.we-wed.ru вы получите всю необходимую информацию об организации свадеб под ключ. Команда профессионалов с вниманием к деталям и с экономией вашего бюджета сделают свадьбу неповторимой. Фотографы, видеографы, стилисты – и все это в команде работающей быстро и с пожеланиями заказчика. Если нужно узнать точную стоимость торжества, необходимо отправить форму и свадебный менеджер оперативно свяжется. Свадебное агентство все заботы по организации торжества возьмет на себя.

  224. Профессиональный ремонт телефонов в г Жуковский с гарантией https://zhukovskiipk.ru/ Вы все еще думаете, что ремонт компьютерной техники стоит дорого?

  226. На сайте http://best-audio-books.ru вы сможете ознакомиться с самыми лучшими аудиокнигами, которые можно слушать ежедневно. Они представлены на любой вкус. И самое важное, что скачивать их можно абсолютно бесплатно и на любое устройство, в отличном качестве. Здесь книги самых популярных авторов, которые вызовут интерес у каждого. Ознакомьтесь с самыми свежими записями, которые добавлены совсем недавно и перепишите произведения на свое устройство. Также опубликованы и свежие комментарии. Для того чтобы подыскать определенную книгу, необходимо ознакомиться с архивами по месяцам.

  227. На сайте https://lovely-professional.ru представлена продукция для наращивания ресниц от проверенных производителей. Купить товары для ресниц можно по низкой цене и с гарантией качества. В каталоге можно найти инструменты для ресниц, клей, косметические средства по восстановлению и уходу бровей и ресниц. Клиентам предлагаются постоянные акции. Широкий ассортимент, конкурентные цены и быстрая обработка – основные критерии интернет-магазина. Оставьте заявку и консультанты помогут подобрать для вас необходимый товар.

  228. На сайте https://coininfor.com/ ознакомьтесь с новостями криптовалютного мира, узнайте прогноз. Весь контент поделен на разделы, чтобы вы быстро сориентировались в доступном материале и ознакомились с тем, что вам действительно интересно. Имеется информация о биржах и о том, как ими правильно пользоваться, какие новшества произошли за последнее время. Обязательно изучите контент, касающийся новых высоких технологий. Вам будут интересны прогнозы, а также аналитические данные. Очень много новостей на эту тему и про майнеров.

  229. На сайте https://auto-arenda-anapa.ru/ возьмите в аренду автомобиль в Анапе. Не потребуются залоги, отсутствуют ограничения. Для того чтобы проверить расценки, необходимо ввести то, в какое время вы планируете взять автомобиль, а также момент окончания аренды. Перед вами большой выбор машин различного класса и уровня. В компании только иномарки. Напротив каждого автомобиля указана стоимость, дополнительная информация, чтобы вы быстро сориентировались в выборе. Каждому клиенту с ребенком предоставляется детское кресло.

  231. На сайте http://bt-futures.ru/ вы получите всю необходимую и актуальную информацию, которая касается бинарных опционов, криптовалютных бирж. Есть полезные данные и о том, как трейдеру начать больше зарабатывать. На сайте находится очень много важного, нужного материала, который будет полезен как новичкам, так и опытным специалистам, которые постоянно развиваются и стремятся всегда быть в курсе последних новостей. Здесь только нужные, актуальные данные, которые помогут лучше разбираться в выбранной сфере.

  232. На сайте https://play.google.com/store/apps/details?id=com.slotsonl1ne.onl1ne5l0t5 вы сможете поиграть в игровые автоматы на деньги. Перед вами только лицензионное казино, где вы сможете попытать свою удачу и выиграть неплохую сумму денег, чтобы заполучить свою мечту. Все автоматы представлены лидерами в своей сфере, а потому точно исключено воздействие на них третьих лиц. За счет огромного ассортимента вы обязательно подберете для себя такой вариант, который позволит вам сыграть на настоящие деньги. А самое главное, что вы сможете заработать средства, почти ничего не вкладывая.

  233. уничтожение тараканов Уничтожение тараканов в Саратовe по низким ценам, хорошие отзывы и гарантия до 1 года. Избавим Вас от прусаков за 1 раз. Полное уничтожение насекомых в квартире. dezses-saratov.ru

  235. На сайте https://btcinfor.com/ ознакомьтесь с интересной, актуальной информацией о том, как развивается биржа криптовалюты. Есть информация не только о биткоинах, но и альткоинах. Составлены специальные разделы под названием «Блокчейн», «Трейдинг». Все статьи написаны высококлассными специалистами – они отлично разбираются в теме, поэтому готовы предложить только самый свежий, интересный и яркий контент. Он будет интересен всем, кто отслеживает информацию. Постоянно появляется новый контент, который обязательно вас впечатлит.

  236. Займы онлайн на карту – это удобный способ решения финансовых трудностей. Независимо от того, нужны вам средства на неотложные расходы или просто дополнительная наличность, мы готовы вам помочь. Заполните заявку на займ, и вам не придется ждать долгих проверок или бумажной волокиты. Деньги поступят на вашу карту в кратчайшие сроки. Займы срочно на карту доступны для всех, без лишних требований к кредитной истории. Получите займ без отказа на карту прямо сейчас и забудьте о финансовых проблемах!

    Рекомендуемые ссылки – займы онлайн на карту

  237. На сайте https://play.google.com/store/apps/details?id=com.SkyyG01fff вы сможете воспользоваться лигой ставок в гольф. Это мобильное приложение позволяет пройти интересные и увлекательные туры. Игра обрадует своим захватывающим сюжетом, оригинальным дизайном. В ней огромное количество лига лунок с интересным и непредсказуемым дизайном. Получится набрать много очков. У приложения приятный и понятный интерфейс, что позволит быстро сориентироваться в игре и получить приятные эмоции.

  238. На сайте https://dimonointeriors.com/ закажите дизайн как коммерческих, так и жилых помещений. Все услуги будут выполнены именно так, как вы хотите и в соответствие с требованиями. Прямо сейчас ознакомьтесь с портфолио, чтобы иметь представление о примерах работ. Вы сможете заказать дизайн апартаментов, частных домов, отелей, офисов, магазинов, медицинских учреждений. Можно оформить интерьер в самом разном стиле, включая минимализм, классику. Каждому клиенту прикрепляется личный менеджер, который будет курировать проект.

  239. На сайте https://bigkurs.ru/ собраны лучшие онлайн-курсы по всем профессиям, которые пользуются огромной популярностью и востребованы на рынке труда. С ними вы сможете обучаться в режиме онлайн. Есть курсы как для начинающих, так и профессионалов. Каждый желающий сможет получить выгодное предложение, воспользоваться курсами от самых популярных школ, которые работают в режиме онлайн. Ознакомьтесь со всеми курсами по психологии. Возможно, вас заинтересуют уроки для работников салона либо визажистов.

  240. На сайте https://meloman.me вы сможете найти приятную и красивую музыку, которая добавит вашему дню позитива, приятных и ярких эмоций. Все треки записаны в отличном качестве, у них четкий звук. Песни лирические, приятные, а потому доставят только положительные и приятные эмоции. Вы сможете скачать песни на любое устройство либо начать прослушивать их в режиме реального времени. Прослушивайте песни на смартфоне, компьютере или любом другом устройстве. Регулярно появляются новые песни, которые точно вам понравятся.

  241. На сайте https://roboty-pylesosy-77.ru/ вы сможете приобрести робот-пылесос. Для всех жителей Москвы и области доступен бесплатный тест-драйв. Вы сможете вернуть устройство, если оно не подошло вам либо не оправдало ожиданий. При этом вам не придется больше думать об уборке, ведь умный и функциональный пылесос сделает все за вас. Все модели имеются в наличии, их можно заказать прямо сейчас. На сайте ознакомьтесь со всеми конструкциями, чтобы выбрать подходящий вариант. Посмотрите видео о правильном использовании устройства прямо сейчас.

  242. Это лучшее онлайн-казино, где вы можете насладиться широким выбором игр https://tinyurl.com/ym6yjz3m и получить максимум удовольствия от игрового процесса.

  243. На сайте https://play.google.com/store/apps/details?id=com.destroyerhrh32 вы сможете сыграть в классическую игру, связанную с уничтожением платформ. Это аркадная игра, которая отличается непредсказуемым, интересным сюжетом. Игрокам нужно будет управлять платформой, а также разрушать блоки, перемещать их поочередно – вправо и влево. Смекалка, тактика и сноровка помогут не пропустить мяч. По мере того, как будете продвигаться, турниры будут все сложнее, а путь – мощнее. Собирайте бонусы, что позволит вам стать сильнее.

  244. На сайте https://rutor.org.ua/ вы сможете скачать видеоматериал по ссылке, а также различные нужные программы, торрент файлы, любые бесплатные программы, которые необходимы вам. Также здесь есть книги, игры – все это представлено абсолютно бесплатно и в отличном качестве. Получится скачать мультики на свой смартфон, чтобы потом посмотреть в любое время, ведь они представлены здесь в огромном многообразии. Регулярно на портале появляются новинки, с которыми необходимо ознакомиться каждому. Обязательно посетите раздел «Разное», который точно вам понравится.

  245. По ссылке https://t.me/liketravelclub воспользуйтесь услугами онлайн-агентства, которое в 2 счета подберет для вас подходящий тур, отель. В компании работают компетентные, высококлассные менеджеры, которые подберут вариант, исходя из ваших предпочтений, финансового положения и других моментов. Вам необходимо лишь обозначить свои предпочтения, требования, после чего менеджер предложит на выбор несколько вариантов. Компания давно работает на рынке, а потому выучила потребности клиента и заслужила доверие.

  246. сэс г Сургут СЭС г Сургут это лучший способ избавиться от клопов и тараканов в квартирах, не прибегая к самостоятельной обработки, что приведет к большой трате денег и бесполезной работе. Все вредители останутся у Вас дома. dezses-surgut.ru

  248. На сайте https://play.google.com/store/apps/details?id=com.balljump.rememberwhat сыграйте в онлайн-казино «Вавада», которое в настоящий момент считается одним из самых популярных заведений. В него играет огромное количество пользователей, которые пытаются сорвать неплохой куш. Заведение всегда предоставляет акции, раздает бонусы, особенно если пользователь только что зарегистрировался. Для получения всех привилегий пройдите регистрацию, на которую потребуется пара минут.

  249. На сайте http://waltzprof.com можно заказать стальной профиль в большом ассортименте. Также здесь есть автоматические выкидные пороги, уплотнители и скрытые петли собственного производства. Компания применяет только современные автоматизированные линии для изготовления качественных, стальных профилей. Есть возможность оформить розничный или оптовый заказ на выгодных условиях. А покупка от производителя – это верное решение экономии на услугах посредника. Если остались вопросы, перезвоните на сайт и менеджеры проконсультируют вас.

  250. На сайте http://abc.informbureau.com вы сможете ознакомиться с экономическими терминами. Такие знания потребуются вам, если преподаете в школе или институте, изучаете экономику или просто решили расширить словарный запас. Словарь содержит все необходимые в обиходе слова. Так вы узнаете о том, что такое «Живые деньги», «Забалансовый счет», «Удержание», «Сальдо» и многое другое. Здесь содержится полный перечень необходимых терминов, которые потребуются вам ежедневно. Почитайте их сейчас, чтобы стать эрудированным.

  252. На сайте https://exclusiveua.com/ ознакомьтесь с информацией, касающейся моды, стиля, красоты. Здесь также представлены эксклюзивные материалы, которые опубликованы только на этом портале. Имеется информация на тему красоты и здоровья, культуры, кухни. И самое важное, что вы обязательно ознакомитесь с лайфхаками, которые пригодятся в обычной жизни. Сайт создан для того, чтобы вы пользовались им регулярно и всегда находили для себя что-то новенькое, свежее и полезное. Регулярно публикуется новая информация, которая будет полезна и вам.

  253. На сайте https://play.google.com/store/apps/details?id=com.slotsonl1ne.onl1ne5l0t5 поиграйте в казино, прочувствуйте эту удивительную атмосферу. Перед вами огромное количество слотов, а также увлекательных азартных игр, которые принесут положительные эмоции. Здесь получится сыграть абсолютно бесплатно и даже получить реальные впечатления. И самое важное, что поиграть можно в любое время, ведь такая игра представлена в мобильном телефоне. Получайте приятные впечатления, даже если вы находитесь в пробке, в очереди.

  255. На сайте https://minervoda.ru/ вы сможете купить Лечебные минеральные воды Чехии. Более 15 лет мы поставляем продукцию в Россию, Белоруссию и Казахстан. Наш ассортимент удовлетворит каждого покупателя, а лечебные свойства воды позволят оставаться здоровым и жизнерадостным. С полной информацией о видах, марках, условиях поставки ознакомьтесь на сайте.

  256. На сайте https://vezuviy.shop/ есть возможность заказать фирменное печное оборудование и дымоходы с высоким качеством гарантии. Если желаете иметь собственный коттедж, либо подыскиваете печь для создания идеального температурного решения, в онлайн-маркете вы найдете то, что вам нужно. Грамотная консультация специалистов даст подробные описания к использованию и установке приборов. Также на сайте есть каталог, с которым можно ознакомиться и подобрать интересующую технику. Клиентам предоставляются выгодные акции и сезонные бонусы.

  257. На сайте https://taker6.casino сыграйте в любопытные слоты, интересные игры, которые вызовут у вас неподдельный восторг и зарядят позитивом. Перед вами огромный ассортимент, что позволит выбрать именно то, к чему тянется душа. Для большей зрелищности создатели предлагают различную бонусную программу, а также проценты по реферальной программе и 100 рублей на счет. Это ведь очень выгодно и главное, что очень вам понравится. Посмотрите, кто выиграл сегодня. Выводите деньги, пополняйте счет тогда, когда вам нужно.

  258. На сайте https://dental-site.ru/ вы сможете заказать уникальный и готовый сайт для стоматологии, который приведет вам первичных пациентов и понравится вашим клиентам. Все сайты адаптированы под смартфоны, легко меняются без программиста и самое важное – это моментальный запуск сайта стоматологии. Ознакомьтесь с ценами на сайты для стоматологии и свяжитесь по контактам указанным на сайте.

  259. На сайте http://na5-ku.ru вы сможете ознакомиться с рейтингом сайтов научных и студенческих работ для того, чтобы подобрать исполнителя на выполнение определенной работы. Напротив каждого пользователя находятся расценки на услуги, а также рейтинг, составленный на основе мнения тех пользователей, которые успели заказать работы. Вы сможете воспользоваться промокодом для того, чтобы услуга стала дешевле. На этом сайте только профессионалы, которые справятся с работой на высоком уровне.

  260. The best blog about travel and food https://www.atravel.blog/ will introduce you to the national cuisine of different countries and unique recipes for dishes from different countries. You can read interesting articles or use ready-made recipes with a unique taste. Discover our blog – it is unique!

  261. На сайте https://soffitto-57.ru/ оформите заявку для того, чтобы заказать ремонтные работы в комнате, квартире, дома, различных помещениях. Рассчитать цену вы сможете прямо сейчас, чтобы заранее спланировать бюджет. Вы сможете воспользоваться самыми разными видами работ, отделки. В бригаде работают лучшие специалисты, которые учитывают предпочтения клиентов, а также технологические нормы. К преимуществам обращения в компанию относят то, что замер, выезд, профессиональная консультация – все это входит в цену.

  262. На сайте https://ecolan37.ru закажите домашний текстиль – привлекательное и износостойкое постельное белье, декоративные подушки, панно из гобелена, стильные простыни, пледы, покрывала, пододеяльники, топперы, наматрасники и многое другое. Вся продукция идеального качества, потому прослужит долгое время, не утратив своего внешнего вида, характеристик. В разделе находятся и товары для бани, а также сауны. Вся продукция реализуется по привлекательным расценкам, с оперативной доставкой, а потому вы обязательно подберете что-то для себя.

  263. На сайте https://m-strop.by/ вы сможете заказать текстильные, грузовые стропы и другого типа. Компания «М-Строп» сама занимается производством стяжных ремней, строп. Вы сможете заказать всю продукцию прямо сейчас и в любом объеме, потому как она хранится на складе предприятия. По этой причине отгрузка происходит максимально оперативно. Оптовые покупатели смогут надеяться на персональные скидки. Оплатить покупку можно наиболее комфортным путем. Доставка осуществляется по всей территории Беларуси.

  264. Буровая компания в Воронеже и области https://vodobur36.ru/ предлагает воспользоваться услугами бурения скважин. Буквально один день и вода на вашем участке будет уже сегодня. Мы первые в своем деле. Все работы проводим качественно, честно. Материалы только ГОСТ и с гарантией. Все работы под ключ и с комплектом документов. Обратитесь к профессионалам и мы поможем пробурить скважину на воду.

  265. На сайте https://play.google.com/store/apps/details?id=com.football.mylineup сделайте ставки в БК «Sportingbet», которая открывает свои двери всем любителям азарта. Компания появилась 15 лет назад и смогла завоевать свою аудиторию. В настоящий момент является лидером беттинга, что подтверждает огромное количество положительных отзывов. Компания регулярно улучшает сервис, чтобы предложить клиентам только лучшее. Услуги предоставляются на 24 языках. Для того чтобы получить доступ ко всему функционалу, необходимо пройти регистрацию.

  266. На сайте https://kg-mashina.ru/ вы сможете купить авто в Бишкеке. Онлайн авторынок в Кыргызстане это большой выбор легковых автомобилей, а также внедорожников, минивенов, мотоциклов, грузовых авто. Воспользуйтесь удобным поиском по сайту и подберите для себя автомобиль по марке или бюджету.

  267. Сайт https://ha-ha.com.ua/ представляет собой уникальный информационный портал, на котором находятся уморительные и смешные ситуации из жизни, но только в картинках. Есть и анекдоты, а также приколы – все то, что обязательно придаст позитива, понравится вам своей неординарностью и необычным подходом. Есть и просто необычные и креативные картинки, которые понравятся всем любителям увлекательных идей. Также представлены и свежие демотиваторы. Есть милые картинки с котиками, другой интересный, полезный контент. К примеру, как выбрать домик для кошки.

  268. На сайте https://krasotulia.com.ua/ почитайте интересные и увлекательные статьи на самую разную тему, включая моду, здоровье, материалы о знаменитостях, также есть рецензии к различным фильмам, новинкам, которые будут интересны и вам. Имеются материалы о культуре: литература, искусство, история. Этот сайт станет вашим надежным проводником в мир интересной, свежей информации. Заходите сюда регулярно, чтобы получить информацию о своей стране. Все статьи составлены высококлассными авторами, которые отлично понимают в данной теме.

  269. На сайте https://xn—-7sba5ajdlcod1ahk.xn--p1ai/ посмотрите телефон компании, чтобы воспользоваться профессиональными и качественными услугами бухгалтерской компании. Она положительным образом зарекомендовала себя на рынке бухгалтерских услуг. В компании работают квалифицированные и первоклассные специалисты, которые помогут решить любую задачу, несмотря на ее сложность. К преимуществам обращения в компанию относят то, что нет необходимости платить зарплату штатному работнику.

  270. Экономический перевод текста Современная экономика характеризуется дальнейшим углублением процессов глобализации. Все чаще предпринимателям и юридическим лицам требуется качественный экономический перевод для заключения контрактов, проведения презентаций, внедрения новых бизнес-схем в деятельность своего предприятия.

  271. The unique sparklo project https://www.sparklo.com/ is a solution for the future for recycling garbage and waste. Look at the detailed information on the website, because the process of sorting, collecting, and recycling waste becomes a simple and exciting activity in which the whole world is interested.

  272. Перевод технической документации Глобализация способствует распространению новых технологий, информация становится все более доступной. Но для того, чтобы воспользоваться ею, нужен технический перевод. Это – одно из самых сложных направлений в работе переводчика, поскольку такие тексты требуют специфических знаний. В нашем бюро работают опытные переводчики, которые справятся с задачами любой сложности.

  273. На сайте https://motovelobike.com.ua/ ознакомьтесь с информацией, которая будет необходима всем, кто желает знать больше о транспорте, различных средствах передвижения. Здесь представлены свежие мотоновости, велоновости, а также автоновости, которые помогут вам получить ответы на многие вопросы. Имеются сведения о подорожании некоторых кроссоверов. Есть данные о Lada Granta, опубликована стоимость нового «Москвича». Обязательно изучите самые свежие, актуальные велоновости, а также последние данные о самых разных машинах. На сайте имеются самые последние данные, которые обязательно вас заинтересуют, если вы являетесь автовладельцем либо только хотите приобрести автомобиль.

  275. На сайте https://cryptotop.info/ изучите ценную и важную информацию, которая касается бирж, криптовалюты, майнинга. Здесь все только интересное, познавательное и увлекательное, что обязательно принесет пользу и поможет расширить кругозор, получить ответы на свои вопросы. Обязательно ознакомьтесь с курсом биткоина и другой криптовалюты. Есть отдельные колонки с новостями, а также публикациями на тему майнинга. Есть просто информативные и познавательные статьи, которые сопровождаются картинками.

  276. На сайте https://taker.website ознакомьтесь со слотами, интересными и любопытными играми, в которые сыграйте в данный момент. Вы сможете испытать свою удачу на любых автоматах. При этом большинство пользователей здесь выигрывают достаточно крупные суммы. Сервис ведет свою деятельность на максимально прозрачных и честных условиях, а потому вывести положенную сумму вы сможете в любое время. Также предусмотрена кнопка и для пополнения баланса. Посмотрите то, кто выиграл сегодня. Возможно, сегодня удача улыбнется вам!

  277. На сайте https://izumrudprint.ru/ узнайте телефон проверенной, качественной типографии, чтобы воспользоваться услугами: печатью журналов, книг, полиграфией, календарей, различной сувенирной продукции. Также здесь можно заказать и различные сувенирные коробки. Все это по привлекательной стоимости, компетентные специалисты укладываются в строго отведенные сроки. Они продумают дизайн и используют только инновационные материалы. По этой причине продукция сохранит свой изначальный вид надолго.

  278. На сайте https://cryptodom.info/ ознакомьтесь с новостями из мира криптовалюты. Есть свежие и актуальные данные на эту тему, а также статьи по трейдингу, технологиям. Вы найдете и курс криптовалюты, последние новости из этого мира и многое другое, что вам обязательно пригодится. Есть данные про самые популярные биржи, высокие и совершенные технологии, а также трейдинг. Есть данные про майнинг и многое другое. Изучите все рубрики, с которыми вы сможете ознакомиться в данный момент. Регулярно публикуется новая информация и актуальные заметки.

  279. На сайте https://vestistroyki.com/ вы сможете ознакомиться с самыми последними новостями из мира строительства. Этот портал посвящен актуальным тенденциям, а также инновациям в этой сфере. Основной принцип издания – предоставить читателям наиболее полную и полезную информацию, которая пригодится при проведении разноплановых работ. В компании работают лучшие журналисты, авторы, которые стремятся расширить ваш кругозор. Они дают важные рекомендации и ценят каждого читателя, чтобы предложить действительно стоящий материал.

  280. в заказах которые ты по всей видимосчти без меня отправлял часто попадается „от Николая“

  281. На сайте https://tehstroy-city.ru/ вы сможете посмотреть телефон для того, чтобы воспользоваться такими услугами, как ремонт офисов, помещений различного назначения, выполнить отделочные работы. Строительная компания выполняет все услуги на высоком уровне, качественно, в строго установленные сроки. Бригады выполнят работы на должном, высоком уровне, потому как все специалисты отличаются необходимой квалификацией для выполнения работ. Подробный прайс-лист указан на сайте. Ознакомьтесь с портфолио прямо сейчас.

  283. Visit https://bestcreditcard.us/ to check out the best credit cards. Find out ratings, read reviews, choose the best credit card with unique conditions. The best credit cards are divided into categories, each with a description, terms, annual rates and other useful information.

  284. На сайте https://portalnovyn.com/ ознакомьтесь с интересными, увлекательными и свежими новостями, которые касаются Украины. Новости на тему экономики, политики, войны, культуры. Есть контент на самые разные темы. Так вы узнаете и мнение первых лиц государства, президента о происходящей ситуации. Имеется информация и про Израиль, США, Румынию. Специалисты отслеживают новости 24/7, чтобы предоставить их в неизменном виде. Все данные актуальные, честные, прозрачные, а потому новостям точно можно доверять.

  285. Visit https://playoffs.hockey/ to find out the 2023 Stanley Cup Playoffs schedule and guarantee tickets to the event with the best prices and convenient viewing locations. Don’t miss your chance to watch your favorite NHL team at the best prices guaranteed.

  286. На сайте https://dominfor.com/ изучите полезную, качественную информацию, которая касается ведения хозяйства, а также ремонта и других моментов. Вы узнаете о том, как правильно обрезать малину и многое другое, что позволит получить хороший урожай. Имеются данные на тему экономики, политики, мнения первых лиц и многое другое, что позволит расширить кругозор и получить более содержательную информацию. Также опубликован контент на тему политики, экономики, финансов. Статьи написаны высококлассными специалистами, которые готовы предоставить важную информацию всем желающим.

  287. На сайте https://play.google.com/store/apps/details?id=com.SkyyG01fff вы сможете сделать свои ставки в БК «Лига ставок», которую основали в 2008 году. Компания считается легальным букмекером, который осуществляет свою деятельность на территории России. Букмекер радует своей лояльностью и особым подходом к ведению бизнеса. Каждый пользователь получает возможность воспользоваться всем функционалом ресурса, чтобы не только заработать денег, но и получить положительные эмоции. Это официальный партнер РПЛ.

  289. На сайте https://nuo.com.ua/ представлена честная, актуальная и интересная информация на самую разную тему, включая детей, культуру, студентов. Обязательно ознакомьтесь с контентом, который точно вам понравится и принесет пользу, расширит кругозор. Также вы узнаете и о том, как справиться со стрессом, о зеленых овощах, которые принесут пользу здоровью. Все статьи свежие, составлены высококлассными специалистами. Они отлично разбираются в теме. Также вы узнаете и о полезных продуктах, которые необходимо употреблять ежедневно.

  291. На сайте https://ukrinfor.com/ вы получите актуальную, нужную информацию на различную тематику: медицина, культура, наука, политика, технологии, спорт. Все статьи очень интересные, увлекательные и понравятся всем, кто отслеживает информацию о своей родной стране. Кроме того, имеются видеоматериалы от ключевых фигур, популярных личностей, которые играют на Украине огромную роль. Все статьи сопровождаются цветными картинками, видеоматериалами, которые помогут лучше понять ситуацию.

  293. Сайт https://bot-glaz-boga-probiv.ru/ это возможность найти или пробить человека из открытых источников и позволяет искать людей, информацию по авто, фамилии и многое другое.

  294. На сайте https://xn--54-6kclv6bgi1b.xn--p1ai/ представлена информация о газовых котлах и комплектующих к ним. Сервис компании предлагает качественные агрегаты по выгодным ценам с оперативной доставкой. Профессиональные специалисты помогут в выборе оборудования и дадут грамотную консультацию. На сайте есть раздел «Вопросы и Ответы», где вы можете узнать интересующую для вас информацию. Также здесь есть удобный каталог товаров, где подробно указаны все характеристики, описания и цены. Если возникли вопросы, менеджеры компании помогут вам в подборе товара и согласовании стоимости.

  295. На сайте https://russianamber.ru/ можно приобрести сувениры и украшения из янтаря по привлекательной стоимости. Представленная коллекция имеет больше 10 тыс. изделий из янтаря. Здесь вашему вниманию предлагаются серьги, колье, броши, кулоны и комплекты украшений. Для удобства оплаты, на выбор есть практически все виды денежных расчетов. Заказ товаров на сайте круглосуточный. Для того чтобы найти товар, необходимо зайти в галерею и ознакомиться с ее содержимым. Далее оформить товар обычным способом.

  296. Технический центр АВ-АВТО https://av-avto.net/ это сервис по ремонту и техническому обслуживанию автомобилей любых марок в Москве. Мы осуществляем капитальный ремонт двигателя, техническое обслуживание авто, ремонт ходовой, компьютерную диагностику, ремонт АКПП, заправку кондиционеров и многое другое. Профессиональные сотрудники, отличные цены, скидки дадут вам возможность недорого и качественно отремонтировать свой автомобиль.

  297. Зайдите на сайт https://rukaster.ru/ и ознакомьтесь с компанией Рукастер в Москве, которая имеет многолетний опыт в предоставлении бытовых услуг, таких как муж на час, мелкий ремонт, электрика, сантехника, сборка мебели и многое другое. Наши специалисты решают различные задачи от ремонта до обслуживания жилых и коммерческих помещений, а вызвать мастера на дом или в офис очень легко и быстро.

  298. На сайте https://ecodok.ru/ вы сможете получить информацию об услугах в области экологии по доступным ценам. Здесь к каждому клиенту находят индивидуальный подход с учетом всех пожеланий и финансовых возможностей. Если вам нужен производственный экологический контроль, либо подготовка к проверке надзорными органами, профессиональные специалисты окажут вам в этом помощь. На портале есть возможность прохождения обучающих курсов, как новичкам, так и опытным сотрудникам. Получите бесплатную консультацию для общения со специалистом.

  299. На сайте https://feringer.shop/ вы найдете актуальную информацию от завода-изготовителя печей, который предлагает полный комплекс товаров. Специалисты проконсультируют, и, если вам необходимо, сделают замеры, а также составят смету. Организуют доставку и установку печи. Каждому покупателю при покупке печи полагается подарок. А для новых и постоянных клиентов действуют акции. Также есть возможность оформления бесплатной доставки по Москве, об этом подробнее рассказывается на сайте.

  300. Интернет магазин https://4766.ru/ лучшие предложения на Webasto EVO, Air Top, а также на автомобильные холодильники Alpicool, лодочные моторы, SUP доски и многое другое. На сайте вы сможете ознакомиться с ценами, описанием, характеристиками товара, а также заказать с доставкой по России или всему миру или забрать самовывозом в Москве.

  301. Сайт https://redrive.world/ это возможность быстро и недорого купить автозапчасти из Польши для немецких автомобилей. Подобрать Запасные части по VIN-коду тоже не составит труда. Переходите не сайт и ознакомьтесь с актуальной информацией о компании, ценами и условиями доставки запчастей.

  303. UGG – это стиль и уют в одном флаконе. Приходите на нашу распродажу 2023 года и купите UGG по самым привлекательным ценам. Вас ждут приятные сюрпризы!

    Сайт: uggaustralia-msk.ru
    Адрес: Москва, 117449, улица Винокурова, 4к1

  304. На сайте https://play.google.com/store/apps/details?id=com.z3r0.her0 есть возможность азартным игрокам прекрасно провести время и заработать. Это большая и авторитетная площадка, где имеется удобный дизайн и щедрая бонусная система. В любое время суток, игроков поддерживает и сопровождает слаженная работа технической поддержки. Здесь есть все, чтобы был обеспечен лучший сервис для виртуальных игр. Rox casino зеркало при его использовании не нужно оформлять профиль заново. Вам нужно только авторизироваться и продолжать играть.

  305. На сайте https://prometall.shop/ представлена информация о полном комплексе услуг по печам. Здесь можно приобрести чугунную печь от производителя по доступной цене. Клиенты компании могут рассчитывать на многие дополнительные услуги, которые касаются банного оборудования и отопления. Также предлагаются скидки и интересные предложения. На сайте есть возможность ознакомиться с каталогом и услугами. Печи компании имеют отличные рекомендации. Цены вас приятно удивят.

  306. На сайте https://kranpioner77.ru/ вы сможете ознакомиться с кранами Пионер, а также арендовать краны по приемлемой цене. Возможна установка других опций, например, колес для перемещения, дополнительного тормоза для лебедки, увеличения глубины опускания. В продаже имеется краны Пионер БУ, полностью исправные и готовые к работе. Все характеристики и цены вы сможете узнать на сайте.

  307. Visit https://www.amcow.org/ to learn about the core functions and mission of AMCOW, an organization that promotes regional and international cooperation through policy coordination and action among African countries on water issues.

  308. Зайдите на сайт https://psyhappy.space/ и познакомьтесь с профессиональным психологом Ростиславом Павловичем, который является врачом и консультантом. Он поможет вам справится с тревогами, забыть о неуверенности в себе, обрести душевное здоровье, поможет с личным развитием или справится со страхами. Онлайн консультации – новая норма поддержки, когда вы имеете индивидуальный подход к беседе, полную анонимность, доброжелательное отношение и работу на результат без эзотерики и ненужных советов.

  310. Зайдите на сайт https://krasnodar-autstaffing.ru/ и ознакомьтесь с компанией Краснодар Аутстаффинг. Мы – это агентство занятости, специализирующееся на работе с иностранными специалистами. Оказываем работодателям консультационную помощь в решении кадровых и миграционных вопросов, помогая снижать расходы на персонал и устранять любые кадровые и миграционные риски. Основные направления это – аутстаффинг мигрантов, миграционный аутсорсинг и консультации экспертов.

  311. На сайте https://play.google.com/store/apps/details?id=com.football.mylineup&gl=br&hl=pt-br есть прекрасные возможности для заработка. Здесь вы найдете много разнообразных сделок. А пользователи будут рады различным акциям и бонусам, в том числе промо-кодов, которые можно получать как вознаграждение за отдельные мероприятия. Пройти активацию очень легко, ну а если вы новичок, то для вас есть специальный приветственный бонус. Техническая поддержка здесь работает круглосуточно, что очень радует игроков. Удобный интерфейс и мгновенные выплаты привлекают пользователей все больше и больше.

  312. The best platform https://ticketregister.us/ for searching and purchasing tickets for any events, be it sports, concerts, shows, musical events. Millions of tickets are available at the best prices, with the best seats guaranteed. You can buy tickets for current events or check out upcoming events.

  314. У меня появилась возможность приобрести уникальный антиквариат, но деньги были нужны срочно. Спасение нашел на cntbank.ru – портале с широким выбором компаний по срочным займам. Акция „займ без процентов“ позволила сделать это выгодно.

  315. На сайте https://apps.apple.com/us/app/vava-circus-da/id6466404651 вы окунетесь в мир увлекательной аркадной игры, где основной задачей является меткость и ловкость. Красочная графика порадует пользователей живописными пейзажами. Здесь есть прекрасная возможность зарабатывать бонусы. Уровни постоянно генерируются, при этом предлагая новые испытания. Соревнуйтесь с другими игроками и устанавливайте свои новые рекорды, зарабатывая достижения. Скачайте игру скорее и погрузитесь в интригующее приключение.

  316. SMART-клиника аппаратной и инъекционной косметологии — VerNa 3 https://verna3.ru/ это услуги высочайшего качества в области инъекционной и аппаратной косметологии, контурной пластики , биоревитализации, плазмолифтинга, нитевого лифтинга, лазерной и аппаратной эпиляции. Мы находимся в Москве, а наш штат состоит из самых высококвалифицированных специалистов.

  317. The theater ticket office https://ticketpayment.us/ will help you get acquainted with all current and future events, as well as easily, in one click, buy tickets to the best places and events. Millions of tickets to local and national events of every kind in 2023 – 2024 at the best prices.

  318. У меня появилась возможность приобрести уникальный антиквариат, но деньги были нужны срочно. Спасение нашел на cntbank.ru – портале с широким выбором компаний по срочным займам. Акция „займ без процентов“ позволила сделать это выгодно.

  319. На сайте https://play.google.com/store/apps/details?id=com.psssoccerstrike вы можете делать винлайн ставки на спорт и получать крупные выигрыши. Каждый клиент включается в программу лояльности. Сайт позволяет осуществлять ставки на все популярные виды соревнований. Здесь постоянно можно видеть разные акционные предложения. Есть возможность просмотра прямых трансляций матчей по футболу, хоккею, баскетболу и другое. Саппорт работает круглосуточно, и готов решить все проблемы, которые у вас возникнут. Для новых клиентов доступен минибонус в виде бесплатной ставки на любой вид спорта.

  320. На сайте https://auto-arenda-anapa.ru/ проверьте цены на прокат автомобилей в Анапе, чтобы прямо сейчас воспользоваться данной услугой. Компания не берет залога, отсутствуют ограничения. Вы сможете выбрать любой автомобиль, который подходит под ваши предпочтения и с учетом определенных технических характеристик. Стоимость автомобилей разная и зависит от того, на какое время вы хотите их арендовать. Некоторые автомобили можно арендовать только с водителем. Отсутствуют ограничения по пробегу, предоставляется детское кресло, регистратор.

  321. Клининговая компания Астра https://astra-clean.ru/ в Санкт-Петербурге – это более 14 лет опыта. Мы оказываем Клининговые услуги для частных лиц и организаций с использованием лучших технологий в области клининга. Посетите сайт, ознакомьтесь с услугами и отличными ценами. Заказывать клининговые услуги у нас – удобно и выгодно, а Индивидуальный подход к каждому заказчику не оставит вас равнодушным.

  323. Продажа бассейнов для загородных участков, оборудования и химии для бассейнов, павильонов и аксессуаров для отдыха бассейн купить доставка плавание – уникальный вид физической нагрузки и упражнений (спорта, в глобальном понимании).

  324. На сайте https://play.google.com/store/apps/details?id=com.sports.c010rj0urney&hl=ru&gl=ru предлагается 1win скачать и получить доступ к функциям и играм. Здесь работает внимательная служба поддержки, которая 24/7 всегда на связи. Сайт позволяет делать ставки, получать бонусы, участвовать в турнирах и акциях, а также обращаться в техподдержку. Качество представленных игр на высшем уровне, а вывод средств происходит мгновенно. Ставки принимаются быстро. Скачать 1win можно как через компьютер, так и через мобильный телефон.

  325. Недавно столкнулся с проблемой освещения в нашем новом доме, особенно в коридоре, где окон нет. Наткнулся на сайт solargy.ru и решил попробовать их световоды. Результат превзошел все ожидания! Теперь у нас естественный свет даже в самых угловых местах.

  326. Оказавшись в непростой ситуации с поломкой моего автомобиля, я поняла, что ремонт обойдется в круглую сумму. На портале cntbank.ru я обнаружила множество компаний по срочным займам. Благодаря акции „займ без процентов“, сумела вовремя отремонтировать машину без переплат.

  327. На сайте https://cec16.ru/ представлена информация о методах уничтожения вредных насекомых, грызунов и плесени. Профессиональные услуги позволят вам устранить проблемы с вредителями в доме, офисе либо коммерческом помещении. Квалифицированные специалисты гарантируют честные цены и безопасность. На сайте есть возможность расчета стоимости обработки. Также здесь предоставляются различные акции. Для того чтобы записаться на обработку, оформите простую заявку на сайте.

  328. На сайте https://mr-shrus.ru/ вы ознакомитесь с информацией магазина, который предлагает большое количество автозапчастей по лояльной цене. Для клиентов подготовлена профессиональная консультация, помощь в диагностике, а также грамотный подбор запчастей. Есть возможность сделать заказ автозапчастей через интернет ресурс. Кроме этого портал предоставляет функцию «Быстрый заказ», при котором покупателю не нужно проходить полную процедуру оформления заказа. Опытные менеджеры подскажут вам о вариантах доставки и оплаты.

  329. На сайте http://semenagrad.ru вы сможете заказать семена почтой. Компания более 30 лет выращивает семена самых разных культур, чтобы предложить вам лучшее качество по доступной цене. Все семена отлично приживаются, потому как наделены безупречным качеством, они отборные и выдерживают различные погодные условия. С помощью «Семенаград» вы сможете обустроить свой участок или сад, посадить на нем различные культуры, чтобы затем получить богатый урожай. Перед вами огромный ассортимент, что позволит подобрать семена, исходя из предпочтений.

  330. На сайте http://mf-podolsk.ru представлены к вашему вниманию кухни на заказ по индивидуальным размерам. Здесь предлагаются самые дешевые решения из современных материалов. Клиент может выбрать фурнитуру, стиль и материалы по своему вкусу и бюджету. Доверьте работу профессиональным специалистам, которые проведут точные замеры помещения, разработают персональный эскиз, соответствующий вашим желаниям. Заказать кухню, а также увидеть 3D конструктор можно на портале.

  331. На сайте https://play.google.com/store/apps/details?id=com.sports.c010rj0urney&hl=ru&gl=ru есть возможность 1win скачать и получить доступ к функциям и играм. Здесь работает лояльная служба поддержки, которая 24/7 всегда на связи. Зарегистрироваться на портале можно на сайте и через мобильное приложение. Для новичков предлагаются промокоды. Качество игр на высоте, а вывод происходит без проблем. Скачать приложение можно легко и просто. Если возникли вопросы, обратитесь в саппорт и вам помогут.

  332. Сломалась кофемашина в Москве? https://coffeedoctor.net/ это ремонт кофемашин в Москве квалифицированными специалистами, с диагностикой и ремонтом и возможностью вызвать мастера на дом или в офис. Мы работаем со всеми известными брендами, имеем склад оригинальных запчастей для кофемашин, даем гарантию на услуги. Мастер кофемашин срочно выезжает в кафе, рестораны, офисы и куда угодно, где вы будете нуждаться в обслуживании и ремонте вашей кофе-техники.

  333. На сайте https://medchina.kz/ вы сможете получить бесплатную консультацию по поводу лечения в китайском государственном военном госпитале. При этом все услуги оказываются без посредников, есть возможность получить консультацию наиболее комфортным для вас способом – через электронную почту либо Вайбер. Для вас действует дисконтная система, которая позволит получить первоклассное лечение с большой скидкой. Постоянно организуются авторские обучающие программы для студентов. В клинике успешно лечатся воспаления, боли.

  334. На сайте https://play.google.com/store/apps/details?id=com.z3r0.her0 можно прекрасно провести время и хорошо заработать. Слоты на портале работают нормально, а вывод денежных средств всегда оперативный. Пользователям нравится привлекательный дизайн, удобная навигация, приятные бонусы и акции. Служба поддержки относится к игрокам дружелюбно, и всегда помогает. Здесь предоставлен лучший сервис для виртуальных игр. Авторизируйтесь и играйте в свое удовольствие.

  335. На сайте https://empathycenter.ru/we-treat/bar/ вы сможете узнать, что такое биполярное аффективное расстройство, его симптомы, причины возникновения, какие используются методы для диагностики. В нашем центре психического здоровья и психологической помощи Эмпатия вы сможете получить квалифицированную консультацию психиатра, а также профессиональное лечение заболевания. Мы используем самые современные и передовые методики.

  336. Сеть отелей на час Апельсин в Москве https://apelsinoteli.ru/ это место которое понравится клиентам. На сайте действует система удобного онлайн-бронирования гостиницы Апельсин с выбором подходящего номера и быстрым внесением сведений о планируемом заезде. Забронировать и снять номер на час или сутки легко, а комфортное оснащение подарят вам уют. У нас охраняемая парковка, Wi Fi, спутниковое ТВ и все что необходимо для комфортного отдыха.

  337. На сайте https://npprteam.shop/ вы сможете купить аккаунты фейсбук и акки ФБ для рекламы, а также арендовать их. Аккаунты отличаются своим качеством и доступностью. В нашем магазине аккаунтов представлен широкий ассортимент товаров.У нас вы можете купить аккаунты фейсбук без зрд и пзрд, трастовые саморег аккаунты facebook фарм, автореги ФБ и google ads, автореги facebook с BM, бизнес менеджер фейсбук, автореги тикток ads и другое.

  338. На сайте https://apps.apple.com/us/app/vava-circus-da/id6466404651 вы можете скачать увлекательную игру уже сейчас. Пользователям предоставляются хорошие бонусы и лояльное отношение службы поддержки. Зарабатывайте бонусы и соревнуйтесь с другими игроками, для достижения новых рекордов. Заходите на портал, скачивайте игру и докажите, что вы мастер оружейной аркады. Понятный и простой интерфейс, красочная графика делают сайт привлекательным для пользователей. Убедитесь в этом и вы.

  339. Зайдите на сайт https://letit.app/ru/ и узнайте об онлайн приложении Letit Traсker, которое сделано трейдерами для трейдеров и поможет улучшить результаты торговли на финансовых рынках. Автоматизированный дневник трейдера безопасен, прибылен, выгоден. Журнал трейдера автоматически собирает, хранит и систематизирует историю торгов, что поможет заниматься продуктивным трейдингом. Ознакомьтесь с полной информацией на сайте.

  341. На сайте https://zamok-ok.ru/vskrytie-avtomobilya/ есть возможность заказать услугу по вскрытию замков автомобиля по приемлемым ценам. Квалифицированные специалисты открывают машину без повреждений в самые короткие сроки. Работают 24/7 и выезжают в любое удобное для вас время. Среднее время работы мастера ? 30 минут. Оговоренная раннее цена не увеличивается по итогу заказа. Клиентам предоставляется гарантия на материалы. С примерами работ, а также услугами компании, можно детальнее ознакомиться на сайте.

  342. На сайте https://orifswe.ru/ вы сможете ознакомиться с интересной, увлекательной информацией о компании Орифлейм, ее продукции. Так вы приобретете все, что хотите и в одном месте. Кроме того, вы всегда сможете изучить актуальный каталог товаров, зарегистрироваться, после чего стать консультантом Орифлейм и получить для себя выгоду при заказе товаров. Теперь заказать продукцию Орифлейм вы сможете в любое время и, не выходя из дома. При производстве продукции используются только инновационные компоненты, которые позволяют получить нужный результат.

  343. Институт психологии и астрологии обучает и выпускает грамотных, профессиональных специалистов https://astroinstitut.ru/obuchenie/ система обучения основана на фундаментальных астрологических принципах.

  346. На сайте https://vezuviy.shop/ есть возможность заказать фирменное печное оборудование и дымоходы с гарантией качества. Компания предлагает приобрести дымоход для печи, нагревательный котел, а также дополнительные аксессуары, которые совместимы с ним на 100%. Если вам нужна консультация от опытных специалистов по установке и использованию печи, обращайтесь, они с удовольствием вам помогут. В разделах каталога есть возможность найти современные печи и порталы для оформления парилки и другое.

  347. Музыкальная школа в центре Уфы для взрослых. У нас не типичные скучные уроки, https://mmotionschool.ru/shkola-barabanov вы сможете погрузиться в захватывающий процесс обучения с лучшими преподавателями!

  349. If you want to know about events and entertainment in Las Vegas, then you will be pleased to visit the website https://2023.vegas/ where you will see the schedule of all current and upcoming events in Las Vegas in 2023. You’ll find your favorite events and can choose great seats and buy tickets to upcoming events at the lowest prices.

  350. На сайте http://moy-dompersonal.ru/ можно оставить заявку на подбор персонала сейчас, и познакомиться с соискателями уже завтра. Агентство недвижимости поможет сэкономить недели на поиске нужного человека. Больше не нужно искать няню либо водителя по знакомым, все эти люди есть в базе. Вам всего лишь нужно отправить заявку. Сроки и условия гарантии зависят от тарифов, с которыми можно ознакомиться на сайте. Если вам нужно лично провести отбор, свяжитесь с менеджерами по телефону и опишите задачу, после чего получите анкету.

  351. На сайте https://farmuzon.net/ вы найдете популярные песни и хиты, которые вам придутся по душе. Музыкальный портал имеет удобный поиск, с помощью которого можно легко отыскать нужную мелодию. Достаточно просто ввести имя исполнителя либо группу, а также название композиции на любом языке. Здесь можно слушать и скачивать mp3 онлайн без проблем. Качество звучания отличное, а огромный выбор музыки позволяет сайту привлекать еще больше пользователей. Любимые треки у вас под рукой, достаточно выполнить несколько кликов.

  352. Перед вступительными экзаменами я обнаружил, что мой аттестат был утерян. В панике я искал варианты, как решить эту проблему. На moskvadiplom.ru я обнаружил именно то, что мне было нужно – аттестат за 11 класс.

  354. На сайте https://gamerguides.ru/ есть возможность ознакомиться с секретами успешной игры. Здесь представлены советы по оптимизации производительности компьютера, секреты удачной игры в многопользовательские и одиночные онлайн-игры, а также информация о получении достижения в играх. Если вы желаете узнать еще больше актуальной информации о гайдах и игровых новостях, то вы обязательно должны посетить данный ресурс. Подписывайтесь на обновления и будьте в курсе новых прохождений.

  355. На сайте https://soberipoke.ru/ можно заказать доставку роллов, поке, смузи по доступным ценам. В ассортименте доставки есть десерты и лимонады на любой вкус, вы обязательно это должны попробовать. При заказе нескольких предложений из меню, вы гарантировано получите подарок. Есть возможность скачать приложение на сайте и получать промокоды, скидки и акции. Меню может отличаться в зависимости от адреса доставки, поэтому обязательно укажите на сайте свой точный адрес.

  356. На сайте https://cryoone.ru/ оставьте заявку на приобретение азотной криокапсулы по доступной цене, которая пользуется большим спросом у клиентов фитнесс центров, салонов красоты, СПА. Работать с криосауной может каждый, вне зависимости от его образования. Если у вас возникли вопросы, пишите, либо звоните и вам помогут. На портале есть возможность ознакомиться подробнее со сферой применения криокапсулы, а также просмотреть видео, фото, галерею и статьи. Начните оформление заказа уже сейчас.

  357. На сайте http://dgchip.ru можно рассчитать стоимость тюнинга двигателя. Для этого необходимо ввести данные по авто и выбрать нужные работы. Компания предлагает разные виды услуг: чип-тюнинг двигателя, отключение мочевины, отключение вихревых заслонок и другое. Здесь можно сделать чип тюнинг двигателей известных марок авто. На сайте есть возможность подробнее ознакомиться с работами компании, а также ценами и услугами. На все виды работ предлагается гарантия и официальные документы.

  358. Visit https://trips.vegas/ for the best tips for planning your trip to Las Vegas. You’ll be able to see the best deals on hotels, packages, shows, concerts, attractions, tours and other activities and things to do and relax. We are the expert guide to Las Vegas.

  359. На сайте http://makeevkainfo.com.ua/ вы ознакомитесь с городскими новостями Макеевки. Здесь есть все: новости, видео, полезные материалы, экономика и многое другое. Новости Макеевки и Украины помогут вам найти свежие обзоры и интервью, а также видео. Разделы на сайте регулярно обновляются. Портал постоянно следит за событиями в городе и стране, и публикует только самые свежие и интересные новости. Сайт очень прост в применении, а удобный поиск дает возможность посетителям быстро найти информацию, которая им интересна.

  360. На сайте https://soccerforma.com/ можно сделать заказ и приобрести футбольную форму высокого качества по приемлемым ценам. Компания предоставляет 100% гарантию на свои изделия, поэтому смело обращайтесь. Работают напрямую с фабриками по производству футбольной формы. Здесь есть удобный поиск, с помощью которого вы быстро найдете нужный товар. Вы можете попасть на распродажу, и выбрать изделие на свой вкус и цвет. Оплата производится при получении, а возврат и обмен – без проблем. Свяжитесь с менеджерами либо оставьте заявку по телефону для заказа.

  361. Однажды у меня внезапно сломалась машина прямо перед важным собеседованием на работу. Мне срочно нужны были деньги на ремонт, и я нашел сайт cntbank.ru, который предложил мне срочный займ на карту. Благодаря быстрому сервису я смог отремонтировать машину и приехать на собеседование вовремя!

  362. На сайте http://profprud.ru можно сделать заказ на готовые пластиковые пруды и материалы для их строительства. Изучите наименование товаров, которых на сайте больше 250. Компания отвечает за качество товаров и предлагает доступные цены. Вы можете связаться с квалифицированными специалистами, которые помогут подобрать подходящее оборудование и дадут детальную консультацию по всем товарным позициям. Также здесь можно найти занимательные статьи и материалы по самостоятельному строительству.

  363. Компания „ПОРАДОМ“ активно работает в сфере строительства и ремонта с 2012 года https://poradom-remont.ru/remont-kvartir Мы предоставляем профессиональные услуги по ремонту и дизайну жилых и нежилых помещений.

  364. On the website https://www.poweronlv.com/ you can get acquainted with the Power-ON project. This is a community mentoring program that aims to empower minors who are at risk of or survivors of commercial sexual exploitation or child sex trafficking.

  365. На сайте https://warsawpoint.com/ вы узнаете последние новости, которые происходят в Варшаве. Здесь речь идет о культурной жизни столицы, об экономики, персонах и политики. На сайте есть удобный поиск, с помощью которого вы легко отыщите нужную информацию. Читайте последние новости на тему в ленте новостей. Сервис объективно предлагает вашему вниманию новости, аналитику и факты. Также на сайте можно добавить свой комментарий. Оставайтесь в курсе событий и отслеживайте обновления всех новостей.

  366. O site https://aviatoraposta.ru/ permite que você aposte na aposta do aviador. As apostas Aviator permitem que você aumente seus ganhos com apostas baixas e dá aos jogadores mais experientes a oportunidade de ganhar mais. Conheça as tarifas no site oficial.

  367. На сайте https://zamok-ok.ru/vskrytie-avtomobilya/ можно узнать актуальную информацию о вскрытии замков автомобиля. Если вы не можете открыть заблокированный автомобиль, обратитесь к профессионалам своего дела, которые грамотно откроют ваше авто без единых царапин и повреждений. Компания дорожит своими заказчиками, поэтому выезжают на заявки в сжатые сроки. На сайте есть возможность подробнее ознакомиться с услугами и преимуществами компании. Они работают круглосуточно и по лояльным ценам, откроют то, что другие не могут.

  368. На сайте https://vavada-zerkalo-site-1.azart.hk/ можно пройти регистрацию и получать выгодные бонусы от игры в казино. Статус дает участникам привилегии при участии в турнирах и увеличение лимита вывода выигрышей. Красивый дизайн радует глаз любого игрока, а развлекательная тема заставит остаться здесь надолго. На портале игры отсортированы по направлениям. Постоянным пользователям нравится удобный функционал и навигация. Вы можете свободно пользоваться сайтом с помощью мобильной версии.

  369. На сайте https://xn—77-6cdfdva6bmwiish9azlhj.xn--p1ai/ вы можете оставить заявку на выполнение кровельных работ под ключ по приятным ценам. Компания предлагает весь спектр услуг, от подбора материалов и проектирования, и до обслуживания и установки кровельных конструкций. Квалифицированные специалисты имеют огромный опыт работы и выполняют ее качественно и с гарантией. На сайте есть возможность связаться с менеджерами для консультации и расчета стоимости работ.

  370. На сайте https://myserial.one/?my=1 вы отыщите популярные, а также новые сериалы. Для того чтобы подобрать подходящий вариант, необходимо воспользоваться фильтром по году, жанру. Есть топ сериалов, которые вызывают интерес у большинства. Все фильмы представлены в безупречном качестве, с хорошим звуком. Их сюжет затягивает, а потому возникает желание их пересматривать постоянно. Ежедневно сериалы обновляются, чтобы предложить вам лучшее. Выбирайте киносериал в зависимости от настроения. Пересматривайте фильмы после работы либо в выходной день.

  371. На сайте https://sng-oil.com/ вы найдете информацию об учебном центре, который выполняет свою работу в сфере охраны труда. Лучшие преподаватели поднимут ваши знания на новый уровень. Здесь вы можете детальнее ознакомиться с обучением и курсами по разным направлениям. Для того чтобы узнать стоимость именно для вас по программам обучения, созвонитесь с менеджером для связи. Обращаясь к ним, вы получите документы по окончанию обучения, а также гарантию и низкие цены.

  372. На сайте https://numerolog56.ru/ вы найдете актуальную и занимательную информацию о нумерологии. Данный портал поможет людям разобраться в себе, где постоянно проводятся тренинги об отношениях, а также есть курсы по нумерологии, в которых разбирают большое количество примеров дат рождении участников. Если хотите построить счастливые отношения, бесплатный марафон на сайте поможет вам в этом. Здесь можно оставить свой комментарий, написав свое имя и электронную почту. Портал имеет удобный интерфейс с рубриками, где каждый найдет что-то полезное для себя.

  373. На сайте Бронируй сам https://booking-ru.ru/ вы сможете легко подобрать для себя тур, купить авиабилеты, подобрать экскурсию или трансфер, купить страховку и почитать об интересных местах в мире. Поиск и бронирование отелей, гостиниц, апартаментов и авиабилетов очень прост и буквально через 1 клик вы забронируете тур своей мечты.

  374. Откройте для себя невероятный мир релакса в Termburg! Наш комплекс предлагает разнообразные термальные ванны, оздоровительные процедуры и массу развлечений для детей и взрослых. Посетите termburg.ru и забронируйте свой отдых уже сегодня!

  375. На сайте https://akcenty.life/ ознакомьтесь с актуальными новостями Киева и всей Украины. Портал разделен на несколько разделов, которые дают возможность быстро и удобно найти необходимую информацию. Здесь вы найдете все о политике, экономике, бизнесе, науке, здоровье и другое. Вся информация достоверная и проверенная. Вы можете подписаться на канал, комментировать его, а также обмениваться опытом с другими пользователями. Будьте в курсе самых свежих новостей и аналитических освещений событий.

  376. Оформление сертификата ИСО 9001 с нами – это не только возможность подтвердить соответствие вашего бизнеса международным стандартам, но оформить сертификат ИСО 9001 и шанс оптимизировать внутренние процессы, повысить уровень управления и улучшить качество услуг.

  378. На сайте https://uanovyny.com/ ознакомьтесь со свежими, актуальными новостями Украины. Они касаются политики, экономики, технологий, здоровья, спорта, культуры. Обязательно ознакомьтесь с курсом валют, а также прогнозом погоды на ближайшее время. Все статьи с картинками, а также видео, чтобы вы смогли лучше понять ситуацию, ознакомиться с ней в полной мере. Изучите новости культуры, спорта. Кроме того, имеются и аналитические данные, статьи, которые составлены специалистами. Имеется раздел с самыми популярными новостями, которые читает большинство.

  379. On the website https://wickedtickets.nyc/ you can discover the untold true story of the Witches of Oz at Broadway’s biggest blockbuster—WICKED, as well as learn about current and upcoming shows for 2023 – 2024 and are guaranteed to buy tickets at the best prices for the best places.

  380. На сайте https://seoforfood.blogspot.com/2007/08/it.html вы ознакомитесь с блогером, который рассказывает о разных историях. Это весьма популярный блог, с необычными случаями из жизни. Здесь каждый отыщет для себя что-то интересное. Рекомендуем вам данный ресурс к ознакомлению. Вы можете подписаться на сообщения и стать постоянным читателем блога. Будьте в курсе историй, в достоверности которых можно не сомневаться. На портале есть популярные сообщения, которые вы можете прочесть уже сейчас.

  381. На сайте https://vpolshe.com/vnzh-v-polshe-karta-czasowego-pobytu/ есть возможность получить консультацию о подаче документов на карту побыту в Польше. Компания занимается подготовкой и подачей пакета документов для получения карты побыту. Персональный подход к вашей ситуацией гарантирован. Для получения карты побыта в Польше, вам достаточно связаться с опытными специалистами компании, для того чтобы они подобрали для вас и вашей семьи оптимальный вариант легализации. На сайте вы можете увидеть отзывы клиентов компании.

  382. Buy tickets to the Gerald Schoenfeld Theater at https://comefromawaytickets.nyc/ Visit the website and get all the information: schedule and tickets. Don’t miss this exciting new musical with unbeatable ticket prices on our website, with the best seats guaranteed.

  383. На сайте https://play.google.com/store/apps/details?id=com.psssoccerstrike есть все для настоящих любителей ставок. Интерфейс интуитивно понятный, а мобильное приложение отменного качества. Саппорт всегда на связи, что не может не радовать. БК винлайн предлагает новичкам приятные бонусы. Скачать приложение можно с планшета либо смартфона. Букмекер старается создавать комфортные условия для пользователей. Осуществлять ставки можно на все популярные виды соревнований.

  384. На сайте https://crawler.wordpress.com/2023/03/15/снежные-забавы/ вы можете увидеть частный блог, где блогер рассказывает разные занимательные истории о жизни. Здесь постоянно добавляются статьи. Если вы любите забавные, реальные истории о жизни, то вам точно понравится. Вы можете добавить свой комментарий к истории. Чем активнее пост, тем больше комментарий. Рассказы все интересные и необычные, здесь каждый найдет что-то для себя. Блогер постоянно выражает свои мысли и впечатления. Заходите на портал и убедитесь в этом сами.

  385. Cntbank.ru обеспечивает прозрачные условия для онлайн займа на карту без скрытых платежей и ограничений. Решение финансовых вопросов теперь не займет много времени и сил. Просто выберите нужную сумму и срок, и деньги будут у вас на карте.

  386. O site https://aviatora-posta.xyz/ é um jogo emocionante onde você pode fazer apostas e, com alto grau de probabilidade, ganhar no aviator aposta mesmo sem qualquer experiência de jogo. O site oficial lhe dirá a estratégia e lhe dará conselhos iniciais sobre a atitude correta em relação ao jogo.

  388. Visit https://beatleslovetickets.com/ to get the best ticket prices for all upcoming The Beatles LOVE concerts at The Mirage, Las Vegas, Nevada. Find out the appropriate date, choose the best ticket and buy it in 1 click with the best price guarantee. Tickets for theater events are already on sale – don’t miss out on unique events.

  389. На сайте https://stas-search.livejournal.com/123236.html вы увидите блог, в котором известный блогер рассказывает интересные истории. Заходя постоянно на портал, вы будете знать, насколько он хорошо ведет страничку, как регулярно выходят его посты, и как он работает с аудиторией. Вы можете подписаться уже сейчас, добавлять свои комментарии, и участвовать. Здесь можно найти кучу всего интересного. Проведите свой досуг вместе с увлекательными постами от блогера и советуйте его своим друзьям.

  390. На сайте https://yumid.ru/ вы можете записаться на прием в клинику и пройти диагностику и лечение по разным медицинским направлениям. Комфортные условия приема, высочайший уровень обслуживания и лечения, конфиденциальность, а также доброжелательный персонал – это главные качества клиники. На сайте можно подробнее ознакомиться со всеми услугами, а также почитать отзывы благодарных клиентов. Записаться на собеседование предлагают уже сейчас. Посетителям дается скидка на прием врача-терапевта.

  391. На сайте https://intersmi.news есть возможность узнать главные события внутри Израиля и за его пределами. Молодая и амбициозная команда портала, имеет достаточный опыт в издании и готова донести до читателей только достоверную информацию. В разделе «Статьи», публикуются интересные аналитические и социально-значимые материалы, которые цитируют ведущие СМИ множество стран по всему миру. Для удобства читателей был разработан уникальный поиск по свежим событиям и новостям.

  394. Apostar em https://aviator-aposta.pro/ aviator aposta é um entretenimento popular em todo o mundo que te tira o fôlego, te mantém em suspense, mas no final, ao receber seus ganhos, você entende que fez o escolha certa. A jogabilidade emocionante e vários bônus tornam o jogo ainda mais interessante.

  399. Сайт https://meatportal.com.ua/ це кулінарні рецепти міжнародної та української кухні, а також кухонні поради про тонкощі утримання будинку, про організацію внутрішнього простору та цікавий блог, який постійно поповнюється цікавими новинами та статтями.

  400. На сайте https://www.avtogalaktika.com/ предлагают выгодное и быстрое оформление кредита под залог вашего авто. После обращения к ним, в течение 30-ти минут вы получите деньги под залог автомобиля удобным для вас способом. Доверьтесь квалифицированным специалистам, которые предложат только лучшие варианты решения финансовых проблем. Если возникли какие-либо затруднения, позвоните по телефонам на сайт, и вам помогут найти вход из трудной ситуации. На портале имеются преимущества ломбарда, а также новости и статьи, с которыми можно ознакомиться уже сейчас.

  401. Сайт https://kissvk.org/ это вся музыка, которую можно слушать или качать бесплатно без регистрации. Подборки песен, хиты 2023 года, новые песни, чарты, альбомы целиком, топ исполнителей, современные тренды, удобный поиск музыки по сайту. Переходи на сайт и слушай, качай любимую музыку.

  402. Стоматологическая клиника в Санкт-Петербурге Тотал Стом https://totalstom.ru/ это профессиональные и качественные услуги по лечению зубов, протезированию, исправлению прикуса, по имплантации зубов. Современная клиника, врачи высшей категории, уютная обстановка – все, что необходимо вам для качественного и безболезненного лечения зубов.

  406. На сайте https://www.m-trud.ru можно сделать заказ на подарочную упаковку из картона по доступной цене. А если вам необходимы подарочные пакеты или эксклюзивные коробки в фирменном стиле, то компания выполнит для вас все по индивидуальным параметрам. Они работают с большими тиражами и принимают штучные заказы. На сайте есть популярные разделы, которые вы можете увидеть уже сейчас, а также подробнее ознакомиться с услугами и продукцией. Немаловажным является и то, что все заказы осуществляются оперативно.

  407. Клиника Стомион в Ставрополе https://stomionclinic.ru/ это стоматология высокого класса, где вы сможете воспользоваться услугами по лечению, протезированию, имплантации зубов, а также по исправлению прикуса. Детская стоматология – это безболезненное лечение зубов у малышей и обучение правильной гигиене.

  408. Сайт https://hitech24.pro/ это полезный портал, где вы сможете найти фото интерьеров, дизайн фото, фото красивого ремонта, фото отделки помещений, стен, потолков, фасадов, ремонт фото и многое другое. Возьмите себе на заметку готовые варианты, а каталог фотографий, составленных по рубрикам это быстрый поиск интересующих вас фото.

  409. На сайте http://ukrnovosti.com.ua представлены последние события в Украине и мире. Здесь есть все, чтобы читатель мог быть быстро и в полной мере информирован. Портал постоянно ищет новые форматы распространения и предоставления информации. Цель сайта – предлагать только достоверную информацию и объяснять важные события активным читателям Украины и мира. Ценностями портала являются репутация, эффективность, развитие, честность и новаторство. На сайте читатель может иметь полное представление о происходящем сегодня и сейчас.

  410. Неожиданно понадобилось оплатить срочный ремонт авто. В этот момент у меня не было свободных средств. Сайт cntbank стал спасением: их список всех займов помог мне быстро сориентироваться и взять займ на карту без лишних проблем.

    Информация о сайте cntbank.ru
    Адрес: 125362, Россия, Москва, Подмосковная ул. 12А.
    Ссылка: список займов на 2023 года

  411. На сайте https://zss22.com/ вбейте название лекарства в поиск заказа нужного продукта для здорового питания. Здесь есть все, что нужно для правильной работы всех органов и систем человека. Вся продукция, сертифицированная, и отмечена наградами, а также медалями. Для консультации со специалистом, заполните форму. Имеется интересная информация для клиентов о компании, с которой можно ознакомиться уже сейчас. Заказать препарат не сложно, достаточно сделать один клик и он окажется в корзине.

  412. Сайт https://1st-car.ru/ это информационный автомобильный портал, который поможет быть в курсе последних автомобильных событий как новичку, так и опытному автовладельцу. Вы узнаете многое из мира автомобилей, почитаете авто журнал, получите консультации по устройству и эксплуатации авто. Сайт постоянно пополняется новыми статьями.

  413. Студия дизайна интерьеров в Екатеринбурге https://studio-mint.ru/ это профессиональные услуги по дизайну и интерьеру квартир и домов, дизайну интерьера коммерческих помещений и офисов, а также индивидуальное проектирование коттеджей и загородных домов, подбор и закуп материалов. На сайте вы сможете узнать стоимость дизайн проекта за 1 минуту.

  415. На сайте https://svoboda.ua вы сможете найти полезную и достоверную информацию о событиях в экономике, политике, спорте, культуре и жизни. В блогах есть возможность почитать мнения корреспондентов и читателей. Вся информация на сайте подразделяется на рубрики для удобства чтения. Здесь каждый найдет что-то для себя интересное. Удобный поиск поможет отыскать нужную информацию в короткие сроки. Добавляйте сайт в закладки и будьте в курсе актуальных новостей первыми.

  416. Студия интерьеров Мята https://studio-mint.pro/ это дизайн, ремонт и комплектация интерьеров под ключ. Профессиональные дизайнерские услуги от нашей студии — это возможность получить качественный ремонт квартир, домов, помещений от лучших специалистов в свой области. Полный перечень услуг, портфолио и интересная информация о нас – на сайте.

  417. Ganhe dinheiro rapidamente https://aviator-aposta.net.ru/ ganhando no aviator aposta, este é um momento de jogo emocionante que você gastará de forma útil no site oficial do jogo do aviador. Mesmo os iniciantes devem tentar, porque muitos profissionais experientes ganham um dinheiro decente com isso.

  418. Однажды у меня сломался ноутбук прямо перед сдачей курсовой. Был в панике, так как нужны были средства на срочный ремонт. На форуме мне посоветовали сайт cntbank. Я перешёл, просмотрел список всех займов на 2023 год и выбрал подходящий вариант. Деньги пришли на карту мгновенно.

    Информация о сайте cntbank.ru
    Адрес: 125362, Россия, Москва, Подмосковная ул. 12А.
    Ссылка: список всех займов МФО

  419. На сайте https://seoforfood.blogspot.com/2009/02/blog-post.html вы ознакомитесь с блогером, который рассказывает о разных историях. Это весьма популярный блог, с необычными случаями из жизни. Здесь каждый отыщет для себя что-то интересное. Рекомендуем вам данный ресурс к ознакомлению. Вы можете подписаться на сообщения и стать постоянным читателем блога. Будьте в курсе историй, в достоверности которых можно не сомневаться. На портале есть популярные сообщения, которые вы можете прочесть уже сейчас.

  420. https://suret.pics/ сайтына өтіп, әртүрлі тақырыптардағы позитивті суреттерді қараңыз. Сіз сондай-ақ күлкілі суреттерді, әдемі суреттерді, құттықтауларды, профильдік суреттерді, күлкілі тағам суреттерін және т.б. таба аласыз. Көңілді және қызықты уақыт өткізіңіз.

  421. Закажите матрешку, посуду, шкатулку с вашей символикой, сюжетом или фото матрешки отбор изделий ведут специалисты с художественным образованием и длительным стажем работы в сегменте подарочной продукции.

  424. На сайте https://cabletrays.moscow представлена широкая база информации о системах кабельных лотков. Информационный портал даст возможность сравнить предложения самых лучших поставщиков и выбрать лояльные условия, уточнить первоначальную стоимость проекта и инжиниринговых работ, а также узнать все особенности монтажа и расчета электрооборудования. Здесь вы получите подробную консультацию квалифицированных специалистов по проектированию кабеля несущих систем.

  425. На сайте https://audiobot.org/ вы сможете скачать музыку с ВКонтакте без установки программ, расширений для браузеров. Скачивайте вашу музыку из ВК в телеграм, на компьютер, телефон или планшет. Огромная коллекция треков, новой музыки, подборки хитов, чарты, альбомы целиком все это на нашем сайте.

  427. Мои родители отмечали золотую свадьбу, и я хотел сделать им приятный сюрприз. На форуме прочитал о сайте cntbank. Список всех займов на сайте помог мне выбрать лучший вариант.

    Информация о сайте cntbank.ru
    Адрес: 125362, Россия, Москва, Подмосковная ул. 12А.
    Ссылка: список онлайн займов

  429. На сайте http://tvoyprud.ru вы ознакомитесь с информацией об оборудовании для прудов, фонтанов и аквариумов. Здесь есть удобный каталог, с помощью которого вы подробнее можно увидеть характеристику товаров и их цены. Также на сайте есть акции, которыми вы уже сейчас можете воспользоваться. Если у вас появилось желание иметь свой собственный пруд, обратитесь в интернет-магазин, гарантирующий качество и приемлемую стоимость. Для заказа товара выберите его и отправьте в корзину, после чего менеджер с вами свяжется и согласует все детали.

  430. Музыка ВКонтакте https://vrit.me/ слушать онлайн или скачать бесплатно. Это многообразие исполнителей, альбомов, треков, певцов, топ чарты, новые исполнители, главные хиты любого года. Удобный поиск музыки, любимых исполнителей, возможность скачать без регистрации все это на нашем сайте.

  431. На сайте https://trollejnyj-shinoprovod.ru оставьте заявку на заказ троллейного шинопровода уже сейчас. Также здесь вашему вниманию предлагается подробное ознакомление информации о троллейных шинопроводах. Вы можете запросить стоимость, оценку проектов и консультирование на электронные адреса, представленные порталом. Каталоги, инструкции, техническая документация шинопроводов разных производителей, даст возможность клиентам детальнее ознакомиться с продукцией.

  432. Ресторан и караоке-бар True Bar https://true-bar.ru/ в Москве на Первомайской и Щелковской это разнообразное меню, ароматные кальяны, стильные и уютные залы, а высокая кухня, безупречный сервис и атмосфера дружелюбия позволит хорошо провести время, а также спеть любимые песни.

  433. Когда моя машина сломалась на полпути к важному собеседованию, я понял, что нужен срочный ремонт. Перерывая форумы, я наткнулся на рекомендацию сайта cntbank. Зайдя туда, я увидел список всех займов на 2023 год. Мгновенная заявка и деньги на карте спасли мой день.

    Информация о сайте cntbank.ru
    Адрес: 125362, Россия, Москва, Подмосковная ул. 12А.
    Ссылка: список всех займов

  435. Наступили холода, и старая куртка уже не справлялась. На форуме один из пользователей упомянул сайт cntbank. Посмотрев список всех займов, я смог найти подходящий вариант и купить новую куртку.

    Информация о сайте cntbank.ru
    Адрес: 125362, Россия, Москва, Подмосковная ул. 12А.
    Ссылка: список займов на карту

  436. Сайт https://taker6.casino/ это увлекательная возможность играть в азартные игры, деля ставки и получая удовольствие от процесса. Выберете любимую игру, получите интересные коэффициенты, бонусы за регистрацию и интересно проводите время. Более подробную информацию вы сможете получить на сайте.

  437. Надоело тратить время на бумажную волокиту и проверки в банках? Ищете быстрый и надежный способ получить финансовую помощь? Тогда наш сервис именно для вас! У нас вы можете получить займы онлайн на карту без проверок в режиме 24/7.

    Процедура максимально упрощена: заполните заявку на сайте, подтвердите свою личность и получите деньги на свою карту. Никаких скрытых комиссий, никаких проверок кредитной истории. Все просто, быстро и надежно.

    Почему же люди выбирают именно нас?

    Без проверок и бумажной волокиты.
    Мгновенное одобрение заявки.
    Возможность взять займ на любую сумму.
    Прозрачные условия и низкий процент.

    Не упустите шанс решить свои финансовые проблемы быстро и без лишних забот.

  438. На сайте https://lilibum.ru есть возможность познакомиться для поиска друзей либо вторых половинок. Бесплатный сайт знакомств дает возможность обмениваться сообщениями, загружать и делиться фото, а также назначать свидания. Широкие возможности ресурса гарантируют интересное общение с людьми и приятное времяпровождение. Здесь продуманная система фильтрации, высокий уровень безопасности и анонимности. Разнообразие анкет и активная аудитория позволяют найти по душе себе собеседника или вторую половинку.

  439. На сайте https://tartugi.net/ есть возможность смотреть онлайн фильмы и сериалы в хорошем качестве. Сделайте просмотр фильмов доступнее, а вечер ? незабываемым. Зритель найдет на портале качественное видео на любой вкус. Если вы не знаете, что выбрать, можете воспользоваться тематическими подборками, либо поиском по параметрам. Популярные сериалы, новинки кино и шедевры кинематографа с известными актерами доступны на всех устройствах. Смотрите с удовольствием, комментируйте и приглашайте друзей на просмотр.

  440. На сайте https://artplay.studio можно оставить заявку и заказать видеопродакшн и анимацию по лояльной цене. Студия поможет представить компанию и привлечь аудиторию с помощью профессиональных видео. Квалифицированные специалисты легко и уверено преподнесут даже самую сложную идею, чтобы добиться хорошего результата. В арсенале студии множество инструментов для презентации продукта клиента. Подробнее ознакомиться с портфолио, а также услугами и ценами студии можно уже сейчас на сайте.

  441. korobok-spb.ru – коробки упаковочные сайт, где вы можете приобрести коробки из гофрокартона по самой выгодной стоимости. Вы можете просмотреть информацию о нужном для вас товаре – стоимость, характеристики, а также условия оплаты. Здесь гарантируют клиентам высокое качество продукции и выполнение заказов точно в установленный срок. Доставка совершается по СПБ и Ленинградской области, также есть возможность отправки товаров в регионы Российской Федерации. Оставьте заявку на портале либо перезвоните менеджеру, чтобы приобрести качественную гофротару.

  442. На сайте https://123film.pro/ вы сможете посмотреть фильмы, новинки сериалов, мультики. Также есть и популярные произведения, которые вам захочется пересматривать раз за разом. Имеются фильмы и сериалы разных жанров: комедии, ужасы, исторические, документальные. Вы сможете воспользоваться фильтром для того, чтобы отсортировать произведения по году и стране выпуска. Среди огромного выбора вы точно подберете вариант, исходя из своих предпочтений и вкуса. Все фильмы в безупречном качестве, с хорошим и четким звуком, а потому точно произведут впечатление.

  445. На сайте http://xn--e1akaddgcecbbo4a.xn--p1ai/ можно вызвать мастера ремонта газовых колонок на дому по приемлемым ценам. Магазин предлагает газовые колонки и материалы к нему по гарантии качества напрямую от производителя. Квалифицированные специалисты быстро выполнят свои услуги. Заявку есть возможность оформить любым способом на сайте. Опытные сотрудники возьмутся за ремонт разной сложности и в любое для вас удобное время. Подробнее ознакомиться с услугами и ценами, вы можете на сайте.

  446. https://mirstroy.by/ – это сайт на котором вы найдете входные и межкомнатные двери по отличным ценам. Металлические двери можно приобрести с установкой и отделкой откос под ключ. На сайте вы найдете строительные услуги такие как кладка блоков, устройство фундаментов, строительство кровли, строительство каркасных домов и пристроек.

  447. Значение и необходимость сертификации ИСО 9001 не поддаются сомнению оформление сертификата ИСО 9001 Получить сертификат ИСО 9001 необходимо, чтобы документально подтвердить тот факт, что предприятия соответствует установленным в стандарте требованиям.

  448. iz-nerzhaveyki.ru – гофрированная подводка сайт, где представлен каталог, в котором вы найдете шаровые краны и гибкую подводку по доступной стоимости. Здесь предлагают только качественную продукцию и гарантируют, что точно останетесь ею довольны. Для оптовых покупателей возможна продажа со скидкой, позволяющей еще больше сэкономить. Купить изделия из нержавеющей стали на оптимальных условиях можно, связавшись с компетентным менеджером. Грамотный специалист подробно расскажет об интересующей вас продукции и посоветует, что именно вам подойдет и почему.

  449. На сайте https://znaya.ru/ представлена подборка курсов по разным интернет-профессиям. Блог поможет найти нужную информацию, и получить все сведения из первых рук. Здесь собрано все в одном месте, инфа актуальная и нужная. Разделы все насыщенные. Данные онлайн-курсы для тех, кто только собирается осваивать удаленную работу, и для тех, кто хочет повысить свой скилл. Каждый сможет выбрать для себя то, что ему необходимо. Удобный интерфейс и поиск поможет быстро подобрать нужную информацию.

  451. На сайте https://minivan.online есть возможность заказать такси минивэн по выгодным тарифам. Вам будут предложены автомобили с откатными дверями с обеих сторон, и с большими креслами для пассажиров. Все водители прошли школу мастерства. На портале опубликованы разные тарифы и показаны способы оплаты, чтобы вы смогли выбрать оптимальный вариант для ваших потребностей. Работают как по предоплате, так и оплате по факту. Также на сайте можно увидеть отзывы и новости компании.

  452. minicamera.ru – wi-fi мини камера сайт, в котором предлагается большой выбор миниатюрных WiFi видеокамер по доступным ценам. Беспроводные камеры работают через приложения для IOS и Android. С помощью него, вы легко сможете настроить камеру под любые задачи. Клиентам предлагаются индивидуальные скидки в зависимости от самого заказа. На ресурсе можно подробнее ознакомиться с каталогом интернет-магазина, также доставкой и оплатой. Если возникли вопросы, перезвоните нам по телефону, указанному на сайте, опытные консультанты помогут вам с выбором.

  453. На сайте https://volman.ru/ вы сможете ознакомиться с последними новостями, дайджестами и статьями о WEB и IT индустрии, а также узнать мнения экспертов по этому поводу. Новостная лента постоянно пополняется, что делает сайт удобным для того, чтобы быть в курсе последних событий из мира IT.

  454. Переезд — это всегда стресс и большие расходы. Когда я переезжал в новую квартиру, я столкнулся с необходимостью оплатить залог, коммунальные услуги и купить новую мебель. Денег, конечно же, не хватало.

    И тут я нашел сайт, который предлагает займ на любую кредитную карту. Этот займ позволил мне сразу оплатить все неотложные расходы и с комфортом обустроить новое жилье. Процесс занял всего несколько минут: заполнить анкету на сайте, подтвердить личность и получить деньги на карту.

  455. На сайте https://oknonovoe.ru/ представлена актуальная информация о пластиковых окнах. Здесь вы узнаете о преимуществах и о выборе правильных материалов для дома. Если желаете знать, какие оконные профили лучше подобрать и как выбрать изоляцию, то блог на сайте точно для вас. Специалисты помогут грамотно разобраться в мире пластиковых окон, а также принять верное решение для вашего жилища. На сайте есть удобный поиск, с помощью которого вы можете выбрать нужную информацию для вас. Если остались вопросы, напишите на портал, и специалисты проконсультируют вас.

  456. Надоело тратить время на бумажную волокиту и проверки в банках? Ищете быстрый и надежный способ получить финансовую помощь? Тогда наш сервис именно для вас! У нас вы можете получить займы онлайн на карту без проверок в режиме 24/7.

    Процедура максимально упрощена: заполните заявку на сайте, подтвердите свою личность и получите деньги на свою карту. Никаких скрытых комиссий, никаких проверок кредитной истории. Все просто, быстро и надежно.

    Почему же люди выбирают именно нас?

    Без проверок и бумажной волокиты.
    Мгновенное одобрение заявки.
    Возможность взять займ на любую сумму.
    Прозрачные условия и низкий процент.

    Не упустите шанс решить свои финансовые проблемы быстро и без лишних забот.

  457. shpargalkin.ru – камера для экзамена сайт, который предлагает купить микрокамеры и микро наушники для сдачи любых экзаменов по лояльной цене. В интернет-магазине можно подобрать товары по своим финансам. Стоимость на комплекты весьма заманчивая. На сайте имеется каталог, с которым можно ознакомиться в любое время. Не пропустите возможность в приобретении наушников и микрокамеры, чтобы ощутить все преимущества уже сейчас. Гарантируем качество и оперативность доставки. Если возникли вопросы, позвоните нам, опытные специалисты дадут консультацию по выбору товаров.

  458. FTBTO https://ftbto.ru/ – юридический справочник в сфере трудовой миграции в Россию, обеспечивающий профессиональную поддержку и консультации. Пишем о миграции и мигрантах, их правах и обязанностях при переезде в Российскую Федерацию.

  459. На сайте https://koinmedya.ru/ вы сможете узнать актуальные новости криптовалют, просматривать данные, котировки, финансовые инструменты, а также последние новости и аналитику. Здесь собрана вся необходимая информация о мировых фондовых рынках, блокчейне, биткоине и многом другом. Эксперты и аналитики следят за самыми важными новостями в мире криптовалют. Читайте обзоры и держите руку на пульсе. Подписывайтесь на рассылку, чтобы не пропустить последние обновления.

  460. Проблема вывоза мусора актуальна не только для жителей больших городов, но и для тех, кто живет в пригороде. В ленобласти, и особенно в гатчинском районе, есть несколько компаний, предлагающих соответствующие услуги. Если вы живете в этом районе и вам нужен вывоз мусора, посетите сайт вывоз мусора в ленобласти гатчинский район. Здесь вы найдете всю необходимую информацию, сможете сравнить цены и выбрать наиболее подходящий для вас вариант.

  461. Цена на вывоз мусора — важный фактор при выборе исполнителя. Она может зависеть от множества факторов: географического расположения, объема мусора, его типа и даже времени года. Чтобы не переплатить и выбрать наиболее выгодный вариант, лучше всего обратиться на специализированный ресурс. На сайте вывоз мусора цена вы найдете актуальные тарифы и сможете сравнить предложения разных компаний. Это поможет сделать правильный выбор и сэкономить.

  462. shkolnaya-parta.ru – стулья для детского сада сайт, где есть возможность купить кресло школьника по приемлемой стоимости. Здесь представлен огромный выбор товаров с доставкой на дом по Москве и другим регионам. Каталог портала постоянно пополняется новейшими моделями и интересными приспособлениями. Для заказа интересующего товара, поместите его в «Корзину» либо позвоните по телефону на сайте, квалифицированные менеджеры помогут вам сделать верный выбор, а также дадут консультации по всем вопросам. На ресурсе вы найдете каталог товаров, а также ознакомитесь с уценками и скидками.

  463. На сайте https://lima161.ru вы можете заказать лимузин, позвонив по номеру телефона. Вашему вниманию предлагаются элегантные и роскошные автомобили. Прокат лимузина пользуется большой популярностью, поэтому, если вы решите воспользоваться данной услугой, позаботьтесь об этом заранее. Посмотреть фотографии экстерьера и внутренней отделки авто, есть возможность в разделе «Автопарк». Цена на прокат лимузина на час представлена на сайте, где также вы увидите фото и контакты компании.

  465. 22 апреля чипмейкер Intel опубликует квартальную отчетность о рынке Forex брокеры в РФ Компания выпустит финансовый отчет после завершения основной торговой сессии на американском рынке.

  467. На сайте https://xakerforum.com/topic/110/page-7 вы можете заказать услуги по взлому страниц почты и детализации смс по приемлемым ценам. Хакер предлагает качественные услуги, которые проводятся анонимно с полной гарантией конфиденциальности для клиента. Он справится с даже самой трудной задачей, вы можете в этом сами убедиться, заказав у него услуги напрямую либо по электронной почте, которая указана на сервисе. Также здесь вы ознакомитесь с ценами специалиста и сможете задать ему свои вопросы, на которые он оперативно отвечает.

  468. На сайте https://ad.kinogid.org вы найдете большое количество кинолент разных жанров. Чтобы подобрать нужный вариант, необходимо воспользоваться удобным фильтром. Портал каждый день обновляется, и добавляются новые фильмы, благодаря чему пользователи могут с комфортом наслаждаться времяпровождением. Все фильмы представлены в отличном качестве и с хорошим звуком. Здесь не надо тратить деньги на регистрацию. Станьте постоянным посетителем портала и смотрите фильмы в любое время.

  470. aifua.com.ua – сайт, на котором можно найти достоверную и актуальную информацию. Вся она организована и разбита на разные тематики. Основные принципы работы ресурса – быстрота и объективность. Ищите новости на тему Білорусь Україна новини ? Здесь есть возможность найти статьи, которые имеют качественные фото и удобны для чтения. Вы можете в любое время ознакомиться с новостями России, Украины и мира. Желаете быть в курсе происходящего первым? С нашим сайтом вы получите доступ к правдивым и подробным сведениям. Материалы о культуре, политике, спорте и экономике уже вас ждут!

  471. На сайте https://lightaudio.ru ознакомьтесь с лучшими новинками за неделю. Вы можете слушать и скачивать совершенно бесплатно на телефон и пк в хорошем качестве. Используя простую и удобную систему поиска, вы с легкостью найдете то, что вас интересует. Наслаждайтесь музыкой у нас и улучшайте свой опыт прослушивания. Все что вам нужно – это зайти на наш музыкальный портал, найти свой трек через поисковую систему либо прослушать последние новинки. Добавляйте нас в закладки, чтобы не потерять сайт.

  472. Вывоз мусора в Санкт-Петербурге регулируется специализированными организациями. Такие компании имеют все необходимые лицензии и разрешения. Если вам нужен надежный и проверенный вариант, обратите внимание на региональный оператор по вывозу мусора в спб. Это гарантия качества и соблюдения всех экологических норм. Вы можете быть уверены, что мусор будет утилизирован правильно и без вреда для окружающей среды.

  473. shemi-otopleniya.ru – сайт, который имеет интересные статьи и предлагает купить по лояльной стоимости гибкую подводку из нержавеющей стали для воды. Ищите купить сильфонная подводка для воды? Здесь предоставляют только лучшую продукцию, широкий выбор ассортимента, высококачественный сервис и индивидуальный подход к каждому клиенту. Постоянно проводятся акции, для того чтобы еще выгоднее были предложения. На профессиональную помощь специалистов можно рассчитывать в любое время, они с большим удовольствием ответят на все ваши вопросы.

  474. На сайте https://arenda.rus.taxi/ вы сможете арендовать авто под такси по выгодным ценам без залога, депозита и первоначального взноса. Все автомобили технически обслужены и исправны. Прозрачные условия аренды, выбор автомобилей от эконом до до комфорт плюс, подключение к агрегаторам такси – все на нашем сайте.

  475. На сайте https://blogodiet.ru/ дана подробная информация про диеты и похудения. Многие девушки и женщины недовольны своим весом: кто-то хочет сбросить вес, кто-то – набрать, ну а кто-то провести разгрузочные дни. В данном блоге ознакомитесь об этих темах поподробнее. В рубрике «Диета» вы узнаете, что нужно кушать, чтобы похудеть, какие есть плюсы и минусы известных диет для похудения. В разделе «Популярные диеты» найдете информацию о том, какие полезные свойства от диеты на основе овощей и фруктов, как нужно питаться перед тренировкой и многое другое. Подписывайтесь на блог и будьте в курсе обновления статей.

  476. m-strop.by – сайт, который предлагает приобрести стропы текстильные, грузовые, канатные и другие грузозахватные приспособления на выгодных условиях. Широкий ассортимент продукции дает возможность удовлетворить даже самых требовательных к качеству покупателей. Для оптовых покупателей предоставляются скидки. Ищите стропы грузоподъемные? На сайте можно найти много полезной информации, ознакомиться с описанием и характеристиками продукции. Если возникнут вопросы, можно позвонить по телефону на сайте и получить квалифицированную консультацию от грамотных специалистов.

  477. На сайте https://sdampodkluch.ru/ речь пойдет о том, как понятно построить дом и сделать качественный ремонт своими руками. Здесь даны советы дизайнеров, которые расскажут, как правильно выбрать дизайн и красиво оформить интерьер вашего помещения. Также ознакомитесь с выбором строительных материалов и инструментов. Сайт разделен на рубрики, для того чтобы пользователям было удобно выбрать то, что им необходимо. Благодаря советам и занимательной информации при подготовке к ремонту, вы станете достойным специалистом, как профессиональные мастера.

  478. На сайте http://www.rp.rv.ua освещаются главные новости Ровно и Украины. Для удобства пользователей был разработан уникальный поиск по свежим событиям. Здесь есть такие разделы новостей: недвижимость, политика, общество, экономика, в мире. Портал всегда стремится к разнообразию материала и формирует у читателя объективное представление о жизни в Украине. Лента новостей дня ? это самые последние и срочные новости в Ровно, Украине и мире. Заходите на сайт и будьте в курсе горячих новостей.

  479. Почему платить за то, что можно получить бесплатно? Наша платформа предлагает вам возможность смотреть бесплатные турецкие сериалы. Здесь нет подводных камней: просто заходите на сайт, выбираете любой из доступных сериалов и наслаждаетесь просмотром. Это идеальный вариант для тех, кто хочет получить доступ к качественному контенту, не тратя при этом ни копейки.

  480. Почему платить за то, что можно получить бесплатно? Наша платформа предлагает вам возможность смотреть бесплатные турецкие сериалы. Здесь нет подводных камней: просто заходите на сайт, выбираете любой из доступных сериалов и наслаждаетесь просмотром. Это идеальный вариант для тех, кто хочет получить доступ к качественному контенту, не тратя при этом ни копейки.

  481. diliht.ru – сайт, который дает возможность приобрести камеры Аквабласта по доступной стоимости, с доставкой по Российской Федерации. Большой опыт работы на разных объектах дает возможность получить грамотную оценку состояния поверхности и предложить персональное и экономически выгодное решение ваших задач. На портале можно детальнее ознакомиться с камерами Аквабластинга, также узнать их описание, характеристики и цену. Ищите станок аквабластинга? Оставьте заявку, либо перезвоните нам по телефонам, и наш специалист проконсультирует вас, а также расскажет об услугах и стоимости.

  482. https://gbisp.ru/keywords/ сайт, где можно приобрести железобетонные изделия по приемлемым ценам. Огромный опыт, а также большое число довольных клиентов, позволяет компании быть лучшей среди сильных на рынке железобетонных изделий. Современное оборудование и постоянные лабораторные проверки гарантируют высочайшее качество бетона. Детальнее ознакомиться с товарами и достоинствами компании можно на портале. С помощью удобного поиска по каталогу можно быстро выбрать необходимую информацию. Закажите у нас обратный звонок, и опытные консультанты помогут вам.

  484. Моя машина неожиданно сломалась прямо перед долгожданным отпуском. Срочно нужен был ремонт, но денег на это не было. Тут как раз нашел кредит онлайн без отказа. Процедура заняла минимум времени, и я смог отправиться в отпуск на своем автомобиле, не беспокоясь о финансах.

  485. Хронически свежие новинки из сео промышленности Seo новости
    Являющийся уникумом а также ясный матерриал, самообновление 2 раза в течение неделю

  486. На сайте https://posdrav-norilsk.ru пользователям представлены голосовые поздравления для любых праздников. Здесь каждый сможет подобрать для себя формат. Доступен выбор таких пожеланий: приколы, пожелания, праздники. Есть категория поздравлений по именам. Заказать данные послания по телефону можно, не выходя из дома, согласитесь, это очень удобно. Отправить голосовое поздравление легко, пара несложных действий и праздничное послание окажется входящим звонком в телефоне получателя. На портале нет никаких ботов, а отзывчивая поддержка всегда на связи.

  488. shemi-otopleniya.jimdo.com – сайт, который имеет интересные статьи и предлагает купить по лояльной стоимости гибкую подводку из нержавеющей стали для воды. Ищите системы отопления коллекторное? Здесь предоставляют исключительно лучшую продукцию, впечатлительный выбор ассортимента, качественный сервис и персональный подход к любому клиенту. Регулярно проводят акции, чтобы сделать еще больше выгодные предложения. Вы можете в любое время рассчитывать на квалифицированную помощь сотрудников, которые с радостью ответят на интересующие вопросы.

  490. На сайте https://taroprivorot.nethouse.ru можно заказать услуги таро-онлайн. Здесь есть возможность выбрать любого специалиста для удобной работы и консультации. Эзотерики позволят вам подготовиться к главным событиям в вашей жизни и внесут необходимые поправки. Они ответят на все вопросы, касаемо личной и деловой жизни, восстановят душевный покой, вернут уверенность и стабильность. Детальнее ознакомиться с услугами и ценами можно на портале. Многолетний опыт и отзывы довольных клиентов, являются гарантией эффективности результатов.

  491. На сайте https://world-cam.ru/ вы сможете посмотреть огромное количество камер онлайн по всему миру. Вы сможете выбрать по категории или стране, по другим параметрам или добавить свою камеру. Веб камеры мира онлайн это отличный способ провести время, в реальном времени наблюдая события в разных уголках мира.

  492. iz-medi.ru – сайт, где есть возможность купить по лояльной цене фитинги, гибкую подводку и шаровые краны из нержавеющей стали. Здесь есть большой каталог с удобным функционалом, который делает выбор быстрым и простым. Ищите труба для теплого пола? Постоянные клиенты могут воспользоваться скидками. Мы даем гарантию на квалифицированное обслуживание, профессионализм и ответственность. Предлагаем качественные товары и различные способы оплаты. Стараемся делать все, чтобы с заказчиками сотрудничество было взаимовыгодным.

  493. На сайте https://serialexpress.ru/ можно найти большой выбор мировых сериалов разных жанров. Здесь вы найдете сериалы и для детей, и для взрослых. Всех их можно заказать по частям и выбрать посезонно. Для этого нужно написать на портал в комментарии к заказу либо на почту. Будьте постоянным клиентом, ведь это выгодно, так как действует накопительная система скидок. Удобный поиск поможет вам найти интересующий сериал или мультсериал. Подробнее узнать об оплате и доставке, а также ознакомиться с каталогом, можно на самом портале.

  494. Время от времени каждому нужно отдохнуть от реальности. Именно в такие моменты я предпочитаю заглянуть на сайт hdserialclub.net, где можно смотреть сериалы онлайн. Этот сайт — настоящий кладезь интересных историй, которые помогают мне расслабиться и переключиться. Что особенно ценно, здесь можно найти сериалы на любой вкус: от драмы до комедии.

  495. На сайте https://pokupka-kvartiri.ru, даны советы, как правильно купить либо продать квартиру. Здесь вы узнаете: как поступить тогда, когда пытаешься приобрести дом или квартиру без риелтора; что нужно делать, после оформления сделки. Эксперты пошагово дадут инструкцию в статье. В разделе налоговый вычет, все о вычетах при сделках с недвижимостью. Если необходимо рассчитать сумму возврата налога при покупке квартиры в ипотеку, вы можете воспользоваться нашим онлайн калькулятором. Также здесь вы подробнее прочтете советы по обустройству дома или квартиры.

  496. На сайте https://masteropulo.ru дана информация о работе архитектурной мастерской. Основным ее направлением является архитектурное проектирование и строительство деревянных объектов. Вы можете обратиться в мастерскую за консультацией перед покупкой участка под застройку. Вам обязательно подберут лучший вариант, рассмотрев все плюсы и минусы: экологию, уровень шума, видовые характеристики, качество почвы, соседние застройки и другое. Помимо прочего, предлагаются услуги технической оценки строительного процесса и построенного объекта.

  497. https://rost-sk.com/ сайт, предлагающий строительство домов и коттеджей по типовым и индивидуальным проектам. Также компания готова взять на себя полный комплекс услуг по строительству, отделке и ремонту. Основая цель их – качественно строить. На выполненные работы гарантия 50 лет. Вы можете получить бесплатную консультацию, а также посмотреть последние работы компании. При заказе строительства дома, клиенты получают авторский индивидуальный дизайн в подарок! Если остались вопросы, позвоните по телефону на сайте, грамотные менеджеры проконсультируют вас.

  498. На сайте https://protara.ru есть возможность приобрести разные варианты пластиковой тары оптом и в розницу по лояльным ценам. Сделать заказ можно быстро и без каких-либо усилий. Вы сами можете выбрать вес продукции, а также форму и назначение ящика. Цены и характеристики товаров, которые указаны на сайте носят информационный характер и даются с целью ознакомления клиентов с ассортиментом представленной продукции. Здесь вы найдете более подробную информацию о доставке, способах оплаты, а также ознакомитесь с акциями.

  499. На сайте https://gidonlines.fun представлены только лучшие сериалы и фильмы, которые можно смотреть абсолютно бесплатно. В базе имеется огромный каталог фильмов и сериалов. Присоединяйтесь к сайту и зовите своих друзей, чтобы вместе отправиться в увлекательный мир кино. Здесь вы всегда будете в курсе последних новинок мира телевидения, а также не пропустите новый эпизод передачи или сериала. Удобный поиск позволит найти тот фильм, который вам нужен. На сайте есть возможность подробнее ознакомиться с жанрами и горячими новинками.

  500. Motti https://www.motti.ru/ это женский сайт обо всем самом интересном. Вы сможете читать и знакомиться со статьями из различных категорий, таких как отдых и путешествия, бизнес и деньги, любовь и семья, дом, ремонт, стройка и множеством других. Новости и события размещаются постоянно, так что скучно никогда не будет.

  501. На сайте https://ef-x.ru вы узнаете все, об эффективных инструментах для недвижимости. Покупатели и собственники могут проверить недвижимость и воспользоваться сборником полезных сервисов проекта. На портале для удобства, есть ипотечный калькулятор для расчетов покупки. Здесь есть полезный сервис, чтобы облегчить поиск и работу с клиентом, а также создать рекламу бренда либо заявить всем о своих услугах. Также на сайте есть возможность оформить электронную подпись для участия в тендерах.

  502. On the website https://fast-change.io/ you can trade your cryptocurrencies as much as you want. A completely legal service for buying and selling cryptocurrency that does not ask for personal data. Fast cryptocurrency exchange is a convenient and fast service.

  504. Рейтинг молотого кофе. Что лучше — арабика, робуста или либерика Отличный кофе топ-10 марок ароматного кофе с характеристиками вкуса и отзывами покупателей

  505. На сайте https://abrazivprom.ru предлагают приобрести промышленное, строительное, бытовое покрасочное оборудование и абразивные материалы по доступным ценам. Специально для вас имеется удобный каталог и большой выбор товаров. Быстрая доставка осуществляется по всей РФ. Технические специалисты компании помогут сделать правильный выбор абразивного материала в соответствии технического задания заказчика. На сайте есть возможность посмотреть видеообзоры инструментов, окрасочного оборудования и абразивных материалов.

  506. На сайте http://rezka-hd.pro можно бесплатно смотреть фильмы онлайн в хорошем качестве и без регистрации. Вам просто нужно зайти на сайт, и выбрать интересующий фильм. Здесь есть возможность воспользоваться удобным поиском по категориям. Смотрите ретро фильмы 1990-х – 2000-х, боевики и драмы. Также есть система поиска по названию, достаточно просто вписать название фильма либо сериала и нажать на Enter. Добавьте сайт в закладки, советуйте друзьям и смотрите фильмы и сериалы только здесь. Приятного просмотра!

  508. Сайт https://game24.space/ это большой выбор рисунков, фонов, обоев на самые разные темы и категории. Зайдите на сайт и ознакомьтесь с большим выбором рисунков, для удобства отсортированных по категориям, а также можно скачать большую коллекцию раскрасок, постеров, плакатов. Самый большой выбор картинок только у нас на сайте.

  509. Я всегда стараюсь быть в курсе новинок кино и телевидения. Поэтому мне было приятно узнать, что на hdserialclub.net уже можно смотреть сериалы 2023 года онлайн. Это отличный шанс заранее ознакомиться с будущими хитами и быть в курсе всех кинематографических трендов.

  510. На сайте https://autoinfa.com, есть все полезное для автолюбителей. Здесь вы найдете и прочитаете интересные материалы автоиндустрии, которые дадут вам знания и большой опыт. Самые популярные темы освещены в виде отдельных статей. Вы можете задать свой вопрос, и эксперты с удовольствием на них ответят. Здесь представлены такие полезные рубрики: выбор и покупка, устройство авто, оборудование, практика ремонта, эксплуатация, каско. Удобный поиск позволит найти то, что вам наиболее интересно.

  513. На сайте https://hotplayer.ru вы можете скачать треки бесплатно и без навязчивой рекламы. Здесь вы погрузитесь в мир музыки и обогатите свои музыкальные впечатления. Каждый день на портале есть возможность слушать новые мелодии и наслаждаться ими. Сайт предлагает возможность удобного поиска, прослушивания и скачивания музыки для любого устройства, имеющего выход в интернет. Тут можно искать треки по названию и исполнителю и следить за обновлениями. Новинки музыки ждут вас уже сейчас!

  514. Для меня очень важно качество контента, который я смотрю. Именно поэтому я выбрала hdserialclub.net, где можно смотреть лучшие сериалы в хорошем качестве. Здесь я всегда уверена, что изображение будет четким, а звук — качественным. Для меня это идеальный вариант для просмотра любимых шоу.

  515. На сайте https://zubshop.ru есть возможность купить стоматологические материалы и оборудование в Санкт-Петербурге по низким ценам. Специалисты компании ответят на все ваши интересующие вопросы и дадут консультацию по каждому виду товара. На портале есть скидки недели, которыми вы можете воспользоваться уже сейчас. Для того чтобы быть в курсе появления новых моделей либо предстоящих скидок, подпишитесь на email-рассылку. Здесь вовремя информируют касательно рассылок распродаж, а также обновления ассортимента.

  516. Салон красоты полного цикла в Москве Рассвет 1905 https://rassvet-1905.ru/ это уникальная возможность получить все услуги для красоты в одном месте. Парикмахер, косметолог, маникюр и педикюр, массаж, солярий, барбершоп, ЭМС-тренировки. Профессиональные мастера и доступные цены – вы обязательно захотите возвратиться снова.

  517. На сайте https://growex-group.ru можно заказать перевозку по лояльным ценам. Профессиональный персонал подберет для вас грамотное решение современной доставки груза по вашему адресу. Логистическая компания оказывает такие виды услуг, как автоперевозки, таможенное оформление, авиаперевозки, складское хранение, морские перевозки. Пользователям дается гарантия на оптимизацию расходов и сохранность груза. Приемлемые цены, отсутствие посредников, консультационные услуги – вот основные преимущества компании. Оставьте заявку для получения бесплатного расчета вашей грузоперевозки уже сейчас.

  519. Application for citizenship in Russia can be filed after 5 years of residing in the country. free slot games In order to apply for Russian Golden Visa, the foreign investor must be at least 18 years old, in a good health and must not have criminal record.

  520. arendayachtsochi.com – сайт блога сочи, в котором можно узнать все о водном транспорте и яхтах. Интересует катер аренда в сочи? Здесь есть возможность узнать, куда отправится на яхте, как и для чего, арендовать яхту, что можно брать напрокат, рекомендации по выбору яхты и другое. Блог представляет собой путевые статьи с разбивкой на рубрики, подробнее с которыми вы ознакомитесь на сайте. Помимо увлекательной и информативной части, на ресурсе увидите достоинства сотрудничества с компанией по аренде яхт. Также пользователи могут оставить комментарий к статье.

  521. Официальный сайт Тейкер https://taker.pet/ это лучшие игры и множество бонусов созданы для веселого развлечения с возможностью заработка! А также большое количество различных промокодов и боунсов.

  522. На сайте https://play.google.com/store/apps/details?id=com.hand23.on05.hand23можно с легкостью сделать ставки на спорт и скачать приложение. Здесь вас ждут лучшие европейские чемпионаты, многообразие ставок на киберспорт, а также высочайшие коэффициенты на топовые матчи. Скачивание приложения является важным шагом для новичков и опытных пользователей, которые хотят насладиться удобством, качеством и безопасностью в мире онайн-ставок. Скачав приложение, вы получите доступ ко всем функциям и возможностям букмекерской компании.

  523. serialexpress.ru – сайт, где можно легко отыскать теленовеллы, мультсериалы, телесериалы и документальные фильмы. Мы часто обновляем ассортимент, у нас есть все, что вам нужно. Предлагаемые нами диски отменного качества, не заедают и хорошо упакованы. Ищите купить русские сериалы? Уверены в том, что вы будете довольны своим приобретением. Цены здесь доступные, а сервис выше всяких похвал. Менеджеры быстро работают, и вежливо относятся к клиентам, вы сами можете в этом убедиться. Заказывайте dvd сериалы почтой и не пожалеете!

  524. Хотите начать делать ставки на спорт? Ваш первый шаг – это Мостбет регистрация в Киргизии. Процесс прост и не займет много времени: перейдите по ссылке, заполните необходимые поля, подтвердите свои данные. Вот и все, теперь вы полноправный участник одной из лучших букмекерских платформ. После регистрации вас ждут приветственные бонусы, акции и лучшие коэффициенты на рынке. Следуйте нашим инструкциям, и начните свой путь к успеху в мире ставок уже сегодня!

  525. На сайте <a https://play.google.com/store/apps/details?id=com.BounceLasserr можно скачать приложение для ставок. Следите за спортивными событиями, но не всегда компьютер под рукой? Установите приложение на свой телефон и делайте ставки на спорт в любом месте. Вы легко сможете отслеживать новинки спорта, и делать ставки где угодно. Приложение является удобным и функциональным. Здесь есть возможность получить дополнительные бонусы, заключать спортивные пари, а также выполнять денежные операции удобным платежным инструментом.

  526. На странице https://vid-st.ru/assortiment/reagenty-protivogololednye/ вы сможете ознакомиться с большим ассортиментом реагентов противогололедных, которые предназначены для полного расплавления снежного покрова. Противогололедные реагенты купить в Москве по 25кг или по 50кг с доставкой и на самовывоз можно у нас. Получите больше информации на сайте.

  527. На сайте https://aviator2023.su есть возможность играть в игру и зарабатывать. Начать игру или скачать ее, вы сможете на официальном сайте. Здесь собран ТОП тактик, на которых можно играть в игру и получать каждый день прибыль. Все стратегии и тактики команда портала проверяет лично. Они сами зарабатывают и помогают получать прибыль игрокам. Все отзывы об игре только положительные, пользователи довольны скоростью выплат. Играйте и получайте прибыль каждый день, но не забывайте, что без стратегии можно уйти в минус.

  529. Абузоустойчивый VPS
    Улучшенное предложение VPS/VDS: начиная с 13 рублей для Windows и Linux

    Добейтесь максимальной производительности и надежности с использованием SSD eMLC

    Один из ключевых аспектов в мире виртуальных серверов – это выбор оптимального хранилища данных. Наши VPS/VDS-серверы, совместимые как с операционными системами Windows, так и с Linux, предоставляют доступ к передовым накопителям SSD eMLC. Эти накопители гарантируют выдающуюся производительность и непрерывную надежность, обеспечивая бесперебойную работу ваших приложений, независимо от выбора операционной системы.

    Высокоскоростной доступ в Интернет: до 1000 Мбит/с

    Скорость подключения к Интернету – еще один важный фактор для успеха вашего проекта. Наши VPS/VDS-серверы, поддерживаемые как Windows, так и Linux, гарантируют доступ в Интернет со скоростью до 1000 Мбит/с, что обеспечивает мгновенную загрузку веб-страниц и высокую производительность онлайн-приложений на обеих операционных системах.

  530. aifua.com.ua – сайт, на котором можно найти достоверную и актуальную информацию. Вся она организована и разбита на разные тематики. Главными принципами работы ресурса является объективность и оперативность. Ищите новости на тему медведчук україна новини ? Здесь есть возможность найти статьи, которые имеют качественные фото и удобны для чтения. У нас можно в любое время ознакомиться с новостями Украины, России и мира. Желаете быть в курсе происходящего первым? С нашим сайтом вы получите доступ к правдивым и подробным сведениям. Материалы о культуре, политике, спорте и экономике уже вас ждут!

  531. Имеется множество автосервисов и технических центров, специализирующихся на обслуживании и ремонте автомобилей Audi и Skoda ремонт skoda Один из таких – автосервис Ауди.

  532. Юридическая компания LEX PRIME https://lex-prime.ru/ в Москве это юридические услуги для физических и юридических лиц. Квалифицированные юристы, огромный опыт судебной практики, постоянное повышение квалификации, работа на результат для клиента делают обращение к нам гарантом успеха вашего процесса.

  533. На сайте https://t.me/s/x1win_russia вы сможете узнать первым информацию, новости популярной БК 1win, которая находится на рынке длительное время и радует огромным количеством развлечений и ставок. Канал создан специально для фанатов этой компании, желающих получить больше важной информации, актуальных данных. Только здесь публикуются самые свежие новости из этой сферы, фотографии, картинки. На сайте вы найдете новые промокоды для новичков, которыми вы сможете воспользоваться при регистрации.

  534. Cel mai prietenos ?i crazy gadget store care i?i va colora experien?a digitala cu emo?ii, stil ?i creativitate trotinete de trucuri Ne-am lansat in martie 2013 ?i am adus cu noi „Festivalul Culorilor”

  535. Спортивные ставки в Украине с каждым годом набирают всё большую популярность, и это неудивительно. Анализируя матчи, игроки развивают стратегическое мышление и принимают решения, основанные на статистике и вероятности. Ставки на спорт в Украине с платформой Мостбет становятся не только увлекательным, но и интеллектуальным занятием. Платформа предлагает широкий арсенал инструментов для анализа: от исторических данных до современных аналитических программ. Это позволяет делать обоснованные ставки, повышая шансы на успех. Мостбет делает ставку на образование своих клиентов, предоставляя доступ к обучающим материалам и аналитическим обзорам.

  537. На сайте https://play.google.com/store/apps/details?id=com.aircraft2323skirmish можно делать ставки онлайн через мобильное приложение от букмекерской конторы. Здесь вы можете испытать атмосферу настоящего казино, не рискуя своими реальными денежными средствами. Откройте для себя интересные возможности и вызовы для развития ваших навыков. Постоянные бонусы, оперативный вывод средств, лояльная служба поддержки, делает букмекерскую контору популярной среди пользователей. В зависимости от вида спорта, игрокам доступны разные акции. Делайте ставки и выигрывайте.

  538. Вот они, горячие степи Казахстана, где каждый болельщик может стать частью чего-то большего благодаря ставкам на спорт в Казахстане от Мостбет. Это не просто ставки, это целая эпопея, где ваши знания спорта и удача плетутся в стратегический танец. Выбирайте из множества доступных событий и делайте свои ставки, ощущая вкус победы с каждым успешным прогнозом. Пусть каждый ваш выбор будет вдохновлен интуицией и анализом, а Мостбет станет вашим верным спутником на этом пути. Здесь вас ждут не только увлекательные матчи, но и возможность стать настоящим чемпионом в мире ставок.

  539. На сайте https://savokhin.ru/ вы сможете познакомиться с Савохиным Константином, который является специалистом по Яндекс Директ. Он профессионально занимается настройкой контекстной рекламы Яндекс Директ и оказывает комплексный подход привлечения клиентов в ваш бизнес. Необходимы клиенты для бизнеса из интернета – тогда обязательно зайдите на сайт.

  540. Казино Вавада предлагает захватывающий мир азартных игр и возможность выиграть большие деньги. Чтобы начать играть, необходимо [url=https://play-casino-vavada.online/]пройти регистрацию в Vavada[/url].
    [url=https://play-casino-vavada.online/]Регистрация в Vavada[/url] очень простая и быстрая.. Вам потребуется заполнить небольшую форму, указав свои личные данные, такие как имя, фамилия, электронная почта и номер телефона. Пожалуйста, убедитесь, что вводите правильные данные, чтобы избежать проблем при выводе выигрышей.
    После заполнения формы вам будет предложено создать уникальное имя пользователя и пароль для входа в ваш аккаунт. Используйте только надежные пароли во избежание потери аккаунта.
    После завершения регистрации вам будет предложено подтвердить свою учетную запись, перейдя по ссылке, которая придет вам на почту. После подтверждения вы сможете войти в свой аккаунт и начать играть в любимые игры в казино Вавада.
    Не забудьте ознакомиться с правилами и условиями казино, чтобы быть в курсе всех требований и ограничений. Важно играть ответственно и устанавливать лимиты для себя, чтобы не превысить свои финансовые возможности.
    Удачи в [url=https://play-casino-vavada.online/]вавада онлайн[/url]! Наслаждайтесь азартом и возможностью выиграть большие призы!

  542. На сайте https://aviator2023.su вы можете узнать важные новости. Ежедневно сотрудники сайта присылают дайджест всего того, что необходимо знать одним письмом. Основная миссия канала – это продвижение демократических ценностей, а также прав человека. Прямой эфир телеканала, интересные статьи и видео вы можете загружать для просмотра офлайн в любое удобное для вас время. Редакторы регулярно отбирают материал, который заслуживает вашего внимания. Делитесь с друзьями и не пропустите интересные новости.

  543. zamok-ok.ru – сайт, предлагающий услуги по оперативному вскрытию замков без повреждений. Интересует такой вопрос как: вскрытие замков пионерский? Опытные мастера имеют широкий спектр навыков, что дает возможность им решать задачи различного уровня сложности. Профессиональные специалисты работают быстро и предложат высокое качество обслуживания по лояльной стоимости. Заявки принимаются по телефону круглосуточно, просто скажите адрес, объясните проблему и дождитесь мастера. Где бы вы не находились специалисты откроют перед вами любую дверь. Доверьтесь нам!

  544. здесь можно произвести кузовной ремонт автомобиля, если он был поврежден в результате аварии или коррозии сервис шкода москва Все работы выполняются высококвалифицированными специалистами с использованием современных технологий и оборудования.

  545. Сайт https://cosmolot.dev/ це ліцензійне онлайн казино, де великий вибір гральних автоматів на різну тематику з великим каталогом азартних ігор, турнірів, лотерей, а також робочим дзеркалом Cosmolot.

  546. flashner.ru – сайт, в котором можно приобрести флешки оптом и внешние аккумуляторы по доступной цене. Компания дает гарантию на качество продукции и сотрудничает исключительно с надежными поставщиками. Доставка продукции осуществляется оперативно, вне зависимости от объема заказа. Интересует чип usb флешки? У нас можно купить недорогую продукцию, нацеливаясь на характеристики, стоимость и обзоры. На ресурсе имеется каталог, с которым можно ознакомиться в любое время. Если вам необходима помощь, позвоните нам, сотрудники помогут с выбором. Доверие – вот главный критерий качества нашей компании.

  547. flowersspb.com – сайт, где можно заказать букеты, цветы, свадебное оформление и подарки по приемлемым ценам. Ищите где магазин живых цветов? Цветочная мастерская предложит вам букеты любой сложности и на любой вкус. Здесь самый внимательный персонал и прекрасные цветы. Если вам нужны услуги для праздничного оформления мероприятия, то наши дизайнеры в оговоренные сроки предложат готовый вариант проекта. Детальнее ознакомиться с услугами цветочной мастерской, можно на сайте.

  549. Фавбет Казіно https://favbet.games/ великий беттінг проект, що працює під ліцензією. Ви зможете дізнатися на сайті плюси та мінуси казино, бонуси, каталог ігор, всі переваги цього казино, які бувають ставки.

  550. https://xn--e1aa2af.xn--p1ai/apostil/ Штамп апостиль на документы в Химках Апостиль – это процедура легализации официальных документов для использования за границей. Представляет собой специальный штамп (печать), который ставится на документы государственных органов, таких как свидетельства о рождении, браке или смерти, дипломы об образовании, выписки из реестров и т. д.

  551. В наше время, когда каждая минута может быть на вес золота, услуга срочные займы на карту мгновенно представляет собой настоящий прорыв в сфере личных финансов. Это не просто способ получить деньги здесь и сейчас, это — символ времени, когда финансовая помощь становится такой же доступной, как и любой другой онлайн-сервис.

    Подобные сервисы особенно ценны для людей, которым необходимо немедленно решить свои финансовые вопросы, будь то оплата счетов, срочные покупки или непредвиденные расходы. Благодаря оперативности и минимуму требований, такие займы становятся все более популярными среди различных слоев населения.

    Несмотря на кажущуюся простоту, пользователю стоит быть внимательным при выборе сервиса для займа. Необходимо внимательно ознакомиться с условиями и удостовериться, что финансовая организация является надежной и имеет все необходимые лицензии. Ведь вопросы безопасности и конфиденциальности в таких сделках играют первостепенную роль.?

  552. mastera.art – сайт, где можно купить и продать предметы искусства. Заниматься творчеством и продажами – задача довольно трудная. Именно поэтому был создан этот ресурс, позволяющий художникам находить ценителей искусства и продавать через сервис свои картины. Здесь можно ознакомиться с каталогом работ художников. Интересует масло? Выбирайте произведения искусства, которые идеально подойдут к вашему дому, либо как подарок друзьям. На сайте есть раздел «Распродажа», где есть возможность купить произведение искусства по скидке.

  553. Хотите освоить искусство шитья, вязания, валяния и других творческих направлений? https://vavilon.co скачайте наши курсы и расширьте свои навыки в широком спектре рукоделия.

  554. Мои планы на отпуск были почти идеальны, но как это часто бывает, последний момент преподнес сюрприз в виде неожиданных расходов. Машина требовала срочного ремонта, и я оказался перед выбором: отказаться от долгожданной поездки или найти деньги. Именно тогда я вспомнил о возможности займов без отказа на любую карту. Без лишних сомнений, я отправил заявку и был поражен, когда увидел, что деньги уже на моей карте. Это был волшебный пендель, который помог мне не только сохранить планы, но и понять, что всегда есть решение.

  555. zamok-ok.ru – сайт, предлагающий услуги по оперативному вскрытию замков без повреждений. Интересует такой вопрос как: захлопнулась дверь? Мастера с большим опытом имеют огромный спектр навыков, что позволяет им решать задачи любой сложности. Квалифицированные сотрудники работают оперативно и предоставят отменное качество обслуживания по выгодной цене. Заявки принимаются по телефону круглосуточно, просто скажите адрес, объясните проблему и дождитесь мастера. Где бы вы не находились специалисты откроют перед вами любую дверь. Доверьтесь нам!

  556. На сайте https://zamok-ok.ru/vskrytie-zamkov/, вы сможете воспользоваться недорогой услугой по вскрытию дверных замков. Опытные мастера компании откроют те замки, которые другие не могут. Если вы не можете войти в офис, либо свой дом, специалисты в любое время приедут к вам и выполнят аварийное вскрытие замков. Работу они осуществляют аккуратно и по заранее оговоренной стоимости. Работают без посредников и выезжают в самые короткие сроки. Подробнее узнать об услугах, а также просмотреть работы специалистов, можете на сайте.

  557. На сайте https://play.google.com/store/apps/details?id=com.cute.ruler можно делать ставки на спорт с высокими коэффициентами и начинать выигрывать. Букмекерская контора предлагает большой выбор игр и добросовестно осуществляет свои обязательства. Одним из главных преимуществ БК является онлайн идентификация игрока. На портале можно почитать отзывы об этой конторе. Здесь очень удобный интерфейс, новичок точно не запутается. Также на сайте можно увидеть раздел новостей со спортивными прогнозами. Служба поддержки работает круглосуточно.

  560. На сайте https://pro-dachnikov.com/ вы сможете увидеть и скачать фото на тему дачи и коттеджа, такие как: фото бани, фото ландшафтного дизайна, фото дачного декора, дизайн дачи фото, как украсить дачу и многое другое. Выберете категорию и посмотрите или скачайте фото всего, что связано с дачей и загородным домом.

  561. Купить бытовку недорого от ведущего производителя по самым низким ценам https://dombitovok.ru/ разумный, выгодный и логичный шаг заказчика без издержек по времени.

  562. flowersspb.com – сайт, где можно заказать букеты, цветы, свадебное оформление и подарки по приемлемым ценам. Ищите где живые цветы спб купить? Цветочная мастерская предложит вам букеты любой сложности и на любой вкус. Здесь только самые красивые цветы и отзывчивый персонал, который грамотно подберет для вас состав и цветовую гамму. Если вам необходимы услуги для праздничного оформления каких-либо мероприятий, то наши дизайнеры в кратчайшие сроки предложат готовый вариант проекта. Детальнее ознакомиться с услугами цветочной мастерской, можно на сайте.

  563. Выгодные предложения по ипотеке на готовое жилье от проверенных банков в 2023 году калькулятор ипотеки подберите для себя самый выгодный вариант ипотеки на готовое жилье.

  566. mastera.art – сайт, на котором можно приобрести и продать предметы искусства. Заниматься творчеством и продажами – задача довольно трудная. Поэтому и был создан данный ресурс, помогающий художникам находить ценителей искусства и продавать собственные картины через сервис. Здесь вы сможете найти каталог, где есть все работы художников. Интересует купить картину маслом на холсте в москве? Выбирайте произведения искусства, которые идеально подойдут к вашему дому, либо как подарок друзьям. На сайте есть раздел «Распродажа», где есть возможность купить произведение искусства по скидке.

  567. «СК Сити Строй“: ваш идеальный ремонт начинается здесь

    Ваш дом — это ваша крепость, и ООО «СК СИТИ СТРОЙ» знает, как сделать его не только красивым, но и функциональным. С нашими ремонтными услугами каждый уголок вашего жилища будет продуман до мелочей. Мы ценим доверие наших клиентов и стремимся превзойти их ожидания, предлагая лучшие решения для жизни и отдыха.

    Наши специалисты учтут все, от общей концепции дизайна до выбора отделочных материалов. Превратить квартиру в дом мечты — это искусство, которому мы отдали многие годы, и мы готовы поделиться этим искусством с вами. Заходите на remont-siti.ru и узнайте, как мы можем помочь вам в создании идеального дома. Мы ждем вас по адресу: г. Москва, ул. Новослободская, д. 20, к. 27, оф. 6, чтобы начать этот творческий путь вместе.

  569. На сайте https://mnogo-dereva.ru/ можно выгодно купить пиломатериалы для строительства бань, домов, беседок и декоративной отделки помещений. Интернет-магазин реализует пиломатериалы от производителей, поэтому покупатели отлично могут сэкономить. Сотрудники подберут для вас добротные стройматериалы и организуют быструю доставку. Также клиентам предлагают акции на товары. Заказать и приобрести пиломатериалы несложно, звоните на сайт и специалисты обязательно вам помогут.

  570. Идеальный дом с идеальным ремонтом от «СК Сити Строй“

    ООО «СК СИТИ СТРОЙ» – это мастерство и качество, воплощенное в каждом квадратном метре вашего дома. Обратившись к нам за услугой ремонт под ключ, вы получите не просто обновление интерьера, но и вдохновение новым пространством, созданным с учетом всех ваших пожеланий. Мы гордимся тем, что предлагаем решения, которые делают жизнь наших клиентов более комфортной и стильной.

    С первого штриха карандаша дизайнера до последнего штриха кисти маляра — ваш проект находится в руках профессионалов. Наша команда заботится о том, чтобы процесс ремонта был для вас приятным и беззаботным. Мы находимся в Москве по адресу: ул. Новослободская, д. 20, к. 27, оф. 6, и с нетерпением ждем встречи с вами для обсуждения вашего проекта. Пусть ваш дом станет источником вдохновения с ООО «СК СИТИ СТРОЙ».

  571. zamok-ok.ru – сайт, предлагающий услуги по оперативному вскрытию замков без повреждений. Интересует такой вопрос как: вскрытие замков пионерский? Опытные мастера имеют широкий спектр навыков, что дает возможность им решать задачи различного уровня сложности. Профессиональные специалисты работают быстро и предложат высокое качество обслуживания по лояльной стоимости. Заявки принимаются по телефону круглосуточно, просто скажите адрес, объясните проблему и дождитесь мастера. Где бы вы не находились специалисты откроют перед вами любую дверь. Доверьтесь настоящим профессионалам!

  573. Льготные программы ипотеки в Москве с господдержкой. Выгодные ставки по кредиту на покупку жилья ипотека в москве оформление ипотеки и проведение сделки онлайн.

  576. flashner.ru – сайт, в котором можно приобрести флешки оптом и внешние аккумуляторы по доступной цене. Компания дает гарантию на качество продукции и сотрудничает исключительно с надежными поставщиками. Доставка продукции осуществляется оперативно, вне зависимости от объема заказа. Интересует флешка 64 гб купить в москве? Вы можете купить недорогую продукцию у нас, ориентируясь на стоимость, характеристики и обзоры. На ресурсе имеется каталог, с которым можно ознакомиться в любое время. Если вам необходима помощь, позвоните нам, сотрудники помогут с выбором. Доверие – это основной критерий качества нашей компании.

  578. Что такое отказное письмо по сертификации и кому оно нужно. Отказное письмо — документ, который подтверждает, что товару не требуется сертификат качества или декларация соответствия https://66.ru/news/misc/245775/ чтобы продавать товары на маркетплейсах, нужно доказать, что продукция безопасна для людей, животных и природы.

  579. Отказное письмо (ОП) – это документ, который удостоверяет, что изделие/товар/материал не подлежат обязательной оценке качества и получению сертификата/декларации в определённой системе как получить отказное письмо отказные письма оформляются в разных сертификационных системах.

  580. На сайте https://sporty24.site/ вы сможете найти огромное количество картинок для веселья. Во всем разнообразии смешные картинки, милые картинки, позитивные картинки, прикольные картинки и многое другое. Вы сможете скачать картинки или просто весело провести время листая большую коллекцию картинок.

  584. flowersspb.com – сайт, где можно заказать букеты, цветы, свадебное оформление и подарки по приемлемым ценам. Ищите где цветочный магазин спб? Цветочная мастерская предложит вам букеты любой сложности и на любой вкус. Здесь самый внимательный персонал и прекрасные цветы. Если вам необходимы услуги для праздничного оформления каких-либо мероприятий, то наши дизайнеры в кратчайшие сроки предложат готовый вариант проекта. Детальнее ознакомиться с услугами цветочной мастерской, можно на сайте.

  585. Выбор лучших турецких сериалов сегодня поражает своим разнообразием. Это и глубокие драмы, и захватывающие исторические эпопеи, и легкие романтические истории. Если вы хотите знать, какие сериалы сейчас на пике популярности, посетите платформу, где собраны лучшие турецкие сериалы онлайн.

    Эти сериалы отличает не только качественный сюжет и профессиональная игра актеров, но и высокий уровень продакшн. С каждым годом турецкий кинематограф развивается, и теперь мы имеем возможность смотреть сериалы, не уступающие голливудским по своему исполнению.

    К примеру, сериалы такие как «Великолепный век» и «Любовь и наказание» уже стали классикой и любимы миллионами. Также не стоит упускать из виду и новинки, которые могут стать вашими новыми фаворитами.

    Таким образом, если вы ищете отличный способ расслабиться и погрузиться в увлекательные истории, то лучшие турецкие сериалы онлайн — это именно то, что вам нужно.?

  589. На сайте https://play.google.com/store/apps/details?id=com.tr4nsfer.overandover можно играть в игру и делать ставки. В линии букмекерской конторы пользователи найдут предложения на все виды спорта и киберспорта. Все игроки могут выбрать на официальном сайте понравившееся предложение и получить специальные бонусы в качестве подарка. Главное достоинство БК – широкое разнообразие ставок. Бонусная программа достаточна, разнообразна, вы может сами в этом убедиться. Для того чтобы играть, необходимо зарегистрироваться.

  591. Каждый человек приходит в этот мир для реализации своего потенциала антон винер биография Важно оказаться в университете, который поможет выполнить эту задачу.

  592. На сайте https://flowersspb.com можно заказать доставку цветов по привлекательным ценам. Опытные флористы-дизайнеры украсят праздники и торжества, а также выполнят красивое оформление офиса, витрин и интерьера. Цветочная мастерская предложит для вас композиции и букеты любой сложности, будь-то день Рождение ребенка, мужские букеты и другое. Закажите букеты по выгодной цене уже сейчас и сделайте праздник для своих близких и друзей. Особое внимание цветочная мастерская уделяет свадебной и траурной флористике.

  594. На сайте https://www.youtube.com/watch?v=cCMiyi1OImk можно отыскать следующие видео: «Обзор и тест красная Багги Жодино 150лс 4×4», «Самодельные койловеры перевертыши от МАЗа на багги +тест», «Обзор недорогой мотосигнализации Thor Review Bike alarms Thor». Кроме этого, вы узнаете, куда же пропал Jeep на 40-х тракторах. Смотрите бесплатно ютуб ролики от начала и до конца. Все без исключения развлекательное видео представлено в отменном качестве и без вирусов!

  595. На сайте http://top-serials.pro/ представлен огромный выбор популярных сериалов на любой вкус. Здесь каждый зритель найдет то, что соответствует его предпочтениям. На портале предлагаются такие жанры сериалов, как: драмы, комедии, фантастика, ужасы, триллеры и многое другое. Младшая аудитория также сможет смотреть мультсериалы и детские сериалы. Сервис постоянно обновляет коллекцию, чтобы зритель мог видеть актуальные и захватывающие сериалы. Подключайтесь к сайту и смотрите лучшие сериалы уже сейчас.

  596. Желаете сэкономить при заказе нужных товаров? И Вам интересны яндекс маркет промокоды 2023 ноябрь? Мы знаем, как это выполнить, и с вами обязательно поделимся. fairless.ru/shop/yandeks-market – известный сайт, основным преимуществом которого является наличие огромного количества уникальных предложений. Сайт отличается удобной навигацией и ненавязчивым дизайном. Специально для пользователей ежедневно размещаем актуальные промокоды Яндекс Маркет, которые доступны бесплатно. Поспешите, время акции ограничено. Покупайте выгодно вместе с нами!